Контрольная работа № 8 по алгебре «Формулы сокращенного умножения» с ответами по УМК Макарычев (Просвещение). Поурочное планирование по алгебре для 7 класса. Глава V. Урок 80. Контрольная работа по теме «Формулы сокращенного умножения». Алгебра 7 Макарычев Контрольная работа 8.

Смотреть Список контрольных по алгебре в 7 классе по УМК Макарычев

Контрольная работа № 8
«Формулы сокращенного умножения»

I. Сообщение темы и цели урока

Цель: проверить знания, умения и навыки учащихся по теме.
Тип урока: урок контроля, оценки и коррекции знаний.

II. Общая характеристика контрольной работы

Контрольная работа составлена в 6 вариантах различной сложности (варианты 1, 2 самые простые, варианты 3, 4 сложнее и варианты 5, 6 самые сложные). При этом сложность вариантов нарастает не очень резко. Каждый вариант содержит 6 задач примерно одинаковой сложности (может быть, несколько сложнее две последние задачи).

При проверке вариантов 1, 2 оценка «5» ставится за правильное решение пяти задач, оценка «4» — четырех задач и оценка «3» — трех задач. Одна задача является резервной (или запасной) и дает некоторую свободу выбора учащимся. При таких же критериях оценки за решение задач вариантов 3, 4 дается дополнительно 0,5 балла, вариантов 5, 6 — 1 балл (т. е. оценку «5» можно получить за правильное решение четырех задач).

III. Контрольная работа в 6 вариантах

   К-8. Вариант 1

1. Запишите в виде многочлена стандартного вида выражение: а) (2а – 3b)²; б) (5х – 3у)(5х + 3у); в) 2а³(а + 2b)².
2. Разложите на множители многочлен: а) 25а² – 16; б) –3х² + 6х – 3; в) 8х³ + у².
3. Решите уравнение (5х + 3)² – (5х – 1)(5х + 1) = 28х + 4.
4. Докажите, что выражение 2х² – 4ху + 4у² может принимать только неотрицательные значения.
5. Постройте график функции у = (х² + 2х + 1)/(х + 1) – 3.
6. Докажите, что число 14⁴ – 145² кратно 3 и 17.

   К-8. Вариант 2

1. Запишите в виде многочлена стандартного вида выражение: а) (3а – 2b)²; б) (3х – 5у)(3х + 5у); в) 3а⁴(2а + b)².
2. Разложите на множители многочлен: а) 9х² – 25; б) –3а² + 6а – 3; в) у³ – 8х³.
3. Решите уравнение (4х + 1)² – (4х + 3)(4х – 3) = 6х – 2.
4. Докажите, что выражение 4х² – 4ху + 2у² может принимать только неотрицательные значения.
5. Постройте график функции у = (х² – 2х + 1)/(х – 1) + 3.
6. Докажите, что число 15⁴ – 168² кратно 3 и 19.

   К-8. Вариант 3

1. Запишите в виде многочлена стандартного вида выражение: а) 2а(3а² – 5b)²; б) (2а – 3b²)(4а² + 6ab² + 9b⁴).
2. Разложите на множители выражение: а) 9(а + 2)² – 4; б) (а – 1)³ + 8а⁶; в) (а – b)² + 2(а – b)(а + 3) + (а + 3)².
3. Решите уравнение (2х – 1 )(4х² + 2х + 1) – 8х(х² – 1) = 3x + 4.
4. Найдите наименьшее значение выражения х² + у² – 6х + 2у + 17.
5. Постройте график функции у = (х² + 4х + 4)/(х + 2) + x – 1.
6. Докажите, что число 14⁴ – 165² + 138² – 107² кратно 31.

   К-8. Вариант 4

1. Запишите в виде многочлена стандартного вида выражение: а) 3b(2а – 3b²)²; б) (3а² – b)(9а⁴ + 3а²b + b²).
2. Разложите на множители выражение: а) 4(b – 3)² – 9; б) (а + 1)³–8а⁶; в) (2а – b)² – 2(2а – b)(а – 1) + (а – 1)².
3. Решите уравнение (2х + 1)(4х² – 2х + 1) – 4x(2x² – 1) = 5x – 2.
4. Найдите наименьшее значение выражения х² + у² – 4х + 6у + 19.
5. Постройте график функции у = (x² – 4х + 4)/(х – 2) + х + 1.
6. Докажите, что число 15⁴ – 186² + 173² – 134² кратно 39.

   К-8. Вариант 5

   К-8. Вариант 6

IV. Подведение итогов контрольной работы

1. Распределение работ по вариантам и результаты решения. Данные о результатах работы удобно заносить в таблицу (для каждой пары вариантов).

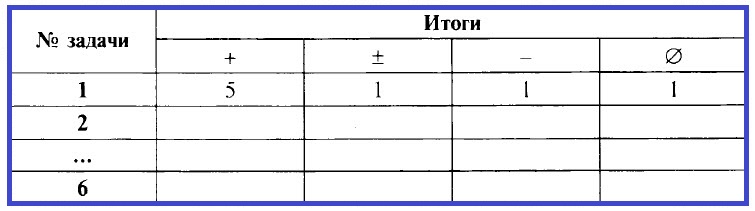
Обозначения:
+ (число решивших задачу правильно или почти правильно);
± (число решивших задачу со значительными погрешностями);
– (число не решивших задачу);
∅ (число не решавших задачу).

2. Типичные ошибки, возникшие при решении задач.
3. Наиболее трудные задачи и их разбор (учителем или школьниками, решившими их).
4. Разбор всей контрольной работы (вывесить на стенде ответы к заданиям и разобрать наиболее трудные варианты).

Алгебра 7 Макарычев Контрольная работа 8

V. Разбор задач (ответы и решения)

Решения и Ответы на вариант 1

№ 1. Запишите в виде многочлена стандартного вида выражение:
а) (2а – 3b)²; б) (5х – 3у)(5х + 3у); в) 2а³(а + 2b)².
ОТВЕТ: а) 4а² –12аb + 9b²; б) 25x² – 9у²; в) 2а⁵ + 8a⁴b + 8a³b².

№ 2. Разложите на множители многочлен: а) 25а² – 16; б) –3х² + 6х – 3; в) 8х³ + у².
ОТВЕТ: а) (5а – 4)(5а + 4); б) –3(х – 1)²; в) (2х + у)(4х² – 2ху + у²).

№ 3. Решите уравнение (5х + 3)² – (5х – 1) (5х + 1) = 28х + 4.
Решение:
(5x + 3)² – (5x – 1) (5x + 1) = 28x + 4
25x² + 9 + 30x – (25x² – 1) = 28x + 4
25x² + 9 + 30x – 25x² + 1 = 28x + 4
2x = – 6
ОТВЕТ: x = – 3.

№ 4. Докажите, что выражение 2х² – 4ху + 4у² может принимать только неотрицательные значения.
Доказательство: Первое и третье слагаемые имеют неотрицательные значения, а второе число определенное значение в таком виде не принимает, поэтому преобразуем выражение:
x² – 4 • x • y + 4 • y² = x² + x² – 2 • x • 2 • y + (2 • y)² = x² + (x – 2y)².
В итоге мы получили сумму квадратов двух чисел. Квадрат любого числа – неотрицательное число, соответственно, сумма квадратов – это также неотрицательное число.

№ 5. Постройте график функции у = (х² + 2х + 1)/(х + 1) – 3.
Подсказка: после сокращения функции постройте график прямой у = х – 2, х ≠ –1.

№ 6. Докажите, что число 14⁴ – 145² кратно 3 и 17.
Доказательство: Раскладываем как разность квадратов:
14⁴ – 145² = (14² – 145)(14² + 145) = (196 – 145)(196 + 145) = 51 • 341 = 17 • 3 • 341.
Кратно, так как у итогового числа есть множители 3 и 17.

Решения и Ответы на вариант 2

№ 1. Запишите в виде многочлена стандартного вида выражение: а) (3а – 2b)²; б) (3х – 5у)(3х + 5у); в) 3а⁴(2а + b)².
ОТВЕТ: а) 9а² – 12ab + 4b²; б) 9х² – 25у²; в) 12а⁶ + 12а⁵b + 3а⁴b².

№ 2. Разложите на множители многочлен: а) 9х² – 25; б) –3а² + 6а – 3; в) у³ – 8х³.
ОТВЕТ: а) (3х – 5)(3х + 5); б) –3(а – 1)²; в) (у – 2х)(у² + 2ху + 4х²).

№ 3. Решите уравнение (4х + 1)² – (4х + 3)(4х – 3) = 6х – 2.
Решение: (4x + 1)² – (4x + 3) (4x – 3) = 6x – 2.
16х² + 8x + 1 – 16x² + 9 – 6x + 2 = 0
Сокращаем и остается 2x + 12 = 0
2x = –12
ОТВЕТ: x = –6.

№ 4. Докажите, что выражение 4х² – 4ху + 2у² может принимать только неотрицательные значения.
Доказательство: Преобразуем выражение:
4х² – 4ху + 2у² = (4x² – 4xy + у²) + у² = (2х – у)² + у².
В итоге мы получили сумму квадратов двух чисел. Квадрат любого числа – неотрицательное число, соответственно, сумма квадратов – это также неотрицательное число.

№ 5. Постройте график функции у = (х² – 2х + 1)/(х – 1) + 3.
Подсказка: после сокращения функции постройте график прямой у = х + 2, х ≠ 1.

№ 6. Докажите, что число 15⁴ – 168² кратно 3 и 19.
Доказательство: Раскладываем как разность квадратов
15⁴ – 168² = (15² – 168) (15² + 168) = (225 – 168) (225 + 168) = 57 • 243 = 3 • 19 • 243
Кратно, так как у итогового числа есть множители 3 и 19.

Ответы на Варианты 3-4

Решения и Ответы на варианты 5-6

Вы смотрели: Алгебра 7 Макарычев Контрольная работа 8 с ответами. Поурочное планирование по алгебре для 7 класса по УМК Макарычев (Просвещение). Глава V. Формулы сокращенного умножения. Урок 80. Контрольная работа № 8 + ОТВЕТЫ.

Смотреть Список контрольных по алгебре в 7 классе по УМК Макарычев