Алгоритмические конструкции
Код ОГЭ: 1.3.2. Алгоритмические конструкции
Различают три основных вида алгоритмов (базовые алгоритмические конструкции, или структуры): линейные, с разветвлениями и с циклами.
В самом простом случае алгоритм предписывает поочередное выполнение всех заданных действий независимо от значений входных данных. Например, чтобы умножить две обыкновенные дроби, необходимо перемножить отдельно их числители и знаменатели и записать их соответственно в числитель и знаменатель результата. Такие действия необходимо выполнять для умножения любых двух обыкновенных дробей.
Алгоритм, предписывающий одноразовое выполнение одной и той же последовательности действий при любых допустимых входных данных, называется линейным (линейной структурой). Использование этой структуры возможно только для простых задач.
Для решения более сложных задач могут потребоваться алгоритмы, предусматривающие два возможных варианта действий. Выбор варианта зависит от некоторого условия. В таких случаях (когда алгоритм реализует выбор одного из альтернативных путей в зависимости от результатов проверки некоторого условия) говорят о ветвлении алгоритма. Например, для решения квадратного уравнения необходимо сначала найти значение дискриминанта, а затем, в зависимости от его знака, либо сообщить об отсутствии действительных корней (если дискриминант отрицательный), либо найти их по соответствующим формулам.
Алгоритм, предписывающий выполнение тех или других действий в зависимости от результата проверки условия, называется разветвленным (структурой ветвления).
Хотя алгоритм ветвления содержит описание действий для обоих возможных вариантов, но при каждом его выполнении реализуется только один из них, какой именно — зависит от заданного набора входных данных. Следовательно, в отличие от линейного алгоритма, при реализации алгоритма с разветвлением будут выполнены не все действия, а только те, что выбраны по условию.
Третий вид алгоритмов (с циклами) обеспечивает многократное выполнение некоторой совокупности действий. Например, для вычисления разности двух чисел в столбик необходимо сначала вычесть последние цифры исходных чисел и записать последнюю цифру результата (если требуется, перенести единицу из предыдущего разряда). Затем аналогично следует вычислить разность предпоследних цифр чисел и так далее. Процедура повторяется, пока все цифры исходных чисел не будут исчерпаны. Количество повторений зависит от количества цифр в заданных числах.
Алгоритм, предписывающий повторное выполнение действий, называется циклическим алгоритмом (алгоритмом с повторением, или структурой цикла).
Повторяемое действие или группа действий называется телом цикла. Количество повторений тела цикла определяется поставленным условием, которое называется условием цикла. По результату проверки условия осуществляется выбор: еще раз повторить тело цикла или перейти к другим действиям.
Наличие возврата к ранее произведенным действиям является характерным отличием алгоритмов с циклами от линейных и разветвленных.
Линейные алгоритмические конструкции
В блок–схемах линейные алгоритмы представляют с помощью последовательности функциональных блоков:

В алгоритмическом языке линейным структурам соответствует последовательность команд языка:
Команда 1
Команда 2
Команда 3
У линейной структуры только один вход и только один выход, попасть извне в середину выполняемой последовательности команд невозможно.
■ Пример 1. Определить значение целой переменной n после выполнения следующего алгоритма:
m := 3
n := 4
m := 6 + m*n
n := n + m/3
Решение. Первые две команды присваивания определяют начальные значения переменных. Для выполнения третьей команды сначала надо вычислить правую часть выражения: 6 + 3 х 4 = 18. Это значение будет присвоено переменной m. Для выполнения последней команды также сначала вычисляется правая часть выражения: 4 + 18/3 = 10. Результат будет присвоен переменной п.
Ответ: 10.
Даже для решения простых задач, ход которого не изменяется в зависимости от исходных данных, могут существовать разные варианты алгоритмов простой линейной структуры.
■ Пример 2. Вычислить значение выражения x2 – 3 × х – 10, используя только операции сложения и умножения.
Для решения задачи в той последовательности, что определяет само выражение, потребуется 2 операции умножения, 2 вычитания и 3 переменных (х, y, z). Однако можно вычислить то же выражение как (х — 2) × х – 10. Такой алгоритм расчета потребует 1 умножение, 2 вычитания и 2 переменных (х, у).
Решение.
Алгоритмические конструкции ветвления
Для отображения базовой алгоритмической конструкции ветвления в блок–схемах используется альтернативный (условный) блок (фигура ромб), а в алгоритмических языках — команда если.
Существует две реализации структуры ветвления: полная и неполная (краткая). Обе формы ветвления являются замкнутыми: каждая из них имеет один вход и один выход.
Полная форма ветвления означает, что осуществляется выбор между двумя действиями. Если проверка условия дает результат «да», то выбирается действие 1; в противоположном случае (то есть если проверка условия дает результат «нет») — выбирается действие 2.
Таким образом, полная форма команды если определяет две ветви команд: первая выполняется, если условие истинно, вторая — если условие ложно. Каждая ветвь в итоге ведет к общему выходу, так что работа алгоритма будет продолжаться при выборе любого пути.
■ Пример 3. Для извлечения квадратного алгебраического корня из числа B необходимо проверить, положительно ли это число. Если проверка дает значение «истина» («да»), извлечь корень; если результат проверки — «ложь» («нет»), выдать соответствующее сообщение пользователю.
Краткая форма ветвления предполагает, что в случае истинности условия будет выполнена команда 1, а иначе — никакие действия не выполняются.

■ Пример 4. Для расчета значений гиперболы по формуле y = 2/x необходимо проверить, что значение х не равно нулю. Если проверка условия дает значение «истина», — вычислить результат. В противном случае (если проверка условия дает значение «ложь», т. е. х равно нулю) — не выполнять никаких действий, поскольку деление на ноль запрещено.
если 2/х ≠ 0
то y := 2/x
всё
■ Пример 5. Для приведенного фрагмента блок–схемы алгоритма выбрать соответствующий ему фрагмент на алгоритмическом языке.
Решение. Ромбу на блок–схеме соответствует структура ветвление (команда если): проверяется условие «отрицательное». Если условие истинно, выполняется ветвь «да» (строка то на алгоритмическом языке) с двумя действиями: «умножить на –1»; «извлечь корень». Если условие ложно, выполняется ветвь «нет» (строка иначе на алгоритмическом языке) с одним действием: «разделить на 2». После обоих вариантов структура завершается, что соответствует служебному слову всё. Такому положению соответствует вариант алгоритма 4.
Ответ: 4.
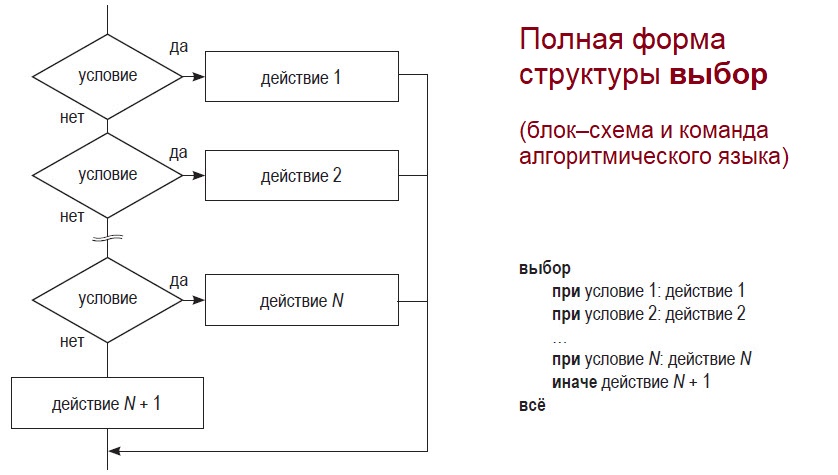
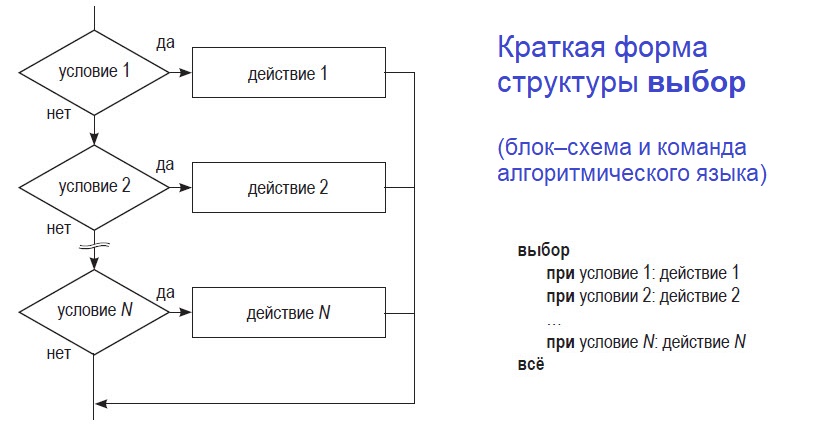
Для серии команд ветвления, следующих одна за другой (множественное ветвление), в алгоритмических языках существуют специальная команда выбор. Она также имеет полную и неполную (краткую) формы.
Структура ветвления выбор предполагает поочередную проверку нескольких условий (одно за одним). Если проверяемое условие 1 истинно, выполняется команда 1, если нет — переходят к проверке следующего условия. Если второе условие истинно — выполняется команда 2, если нет — проверяют следующее условие и т. д.
Полная и краткая формы структуры выбор различаются действиями после проверки последнего условия. Если проверка последнего условия выдает «ложь» («нет»), — в полной форме выполняют заданную команду; в краткой форме ничего не делают.
Во всех формах структур ветвления важную роль играют условия выбора. Часто в них используются операторы сравнения или другие отношения. Результатом условия может быть только одно из двух логических значений — Ложь или Истина. В языках программирования эти значения обычно записывают как True и False. В учебном алгоритмическом языке используют чаще значения «да» и «нет». В компьютерной форме эти значения обычно представлены битовыми значениями 0 и 1.
Простые условия обычно содержат только одну операцию — например, X > 0, А ≠ В или s = «отец». Объединение нескольких простых условий образует составное условное выражение (или составное условие). Для объединения простых условий используются логические операторы:
and (логическое И),
or (логическое ИЛИ),
xor (исключающее ИЛИ),
not (отрицание).
Например, чтобы задать условие принадлежности числовой величины Z промежутку (10;20), следует записать составное условие Z > 10 and Z < 20.
Циклические конструкции
Базовая структура цикл (или повторение) обеспечивает многократное выполнение одних и тех же команд. Существует несколько разновидностей циклических структур. Любая из них содержит тело цикла (набор повторяющихся команд) и заголовок цикла, который определяет количество повторений тела цикла.
ЦИКЛ С ПРЕДУСЛОВИЕМ (ИЛИ ЦИКЛ «ПОКА»)
Заголовок этой структуры содержит условие, которое называется предусловием. Эта структура предписывает повторять тело цикла до тех пор, пока выполняется условие в его заголовке (т. е. пока оно остается истинным).

Работа цикла с предусловием начинается с проверки условия в его заголовке. Если условие истинно — выполняются команды тела цикла и происходит возврат к заголовку цикла. Снова проверяется условие заголовка (поскольку оно могло измениться в результате работы команд цикла) — если оно истинно, опять выполняется тело цикла. Так происходит до тех пор, пока проверка условия в заголовке не выдаст результат «нет». Тогда управление будет передано команде, следующей непосредственно за циклом.
Возможна ситуация, когда команды тела цикла не будут выполнены ни разу — если условие в заголовке сразу же выдает результат проверки «нет». Также возможна ситуация, когда условие заголовка всегда выдает положительный результат проверки — это приведет к бесконечному выполнению цикла, так называемому «зацикливанию» алгоритма. Таким образом, при создании цикла «пока» следует обращать особое внимание на формулировку условия в его заголовке.
■ Пример 6. Записать на алгоритмическом языке алгоритм получения остатка от деления целого числа а на целое число b с помощью вычитания.
Решение. Если число а меньше b, то остатком от деления служит само число а. В ином случае необходимо вычитать b из числа а до тех пор, пока результат не станет меньше b — он и будет остатком от деления.
ЦИКЛ С ПОСТУСЛОВИЕМ (ИЛИ ЦИКЛ «ДО»)
Постусловие формулируется противоположным образом по отношению к предусловию. Цикл «до» предписывает повторять команды тела цикла до тех пор, пока не выполнится условие в его заголовке (т. е. пока оно остается ложным).

Работа цикла с постусловием начинается с выполнения команд тела цикла. Затем проверяется условие цикла. Если условие ложно (проверка условия дает результат «нет») — происходит возврат к выполнению команд тела цикла. Затем снова проверяется условие (поскольку оно могло измениться в результате работы команд цикла). Так происходит до тех пор, пока проверка условия не выдаст результат «да». Тогда происходит выход из цикла и управление будет передано команде, следующей непосредственно за циклом.
В отличие от цикла с предусловием, тело цикла «до» всегда выполняется хотя бы один раз (до первой проверки). Тело цикла «пока» может не выполниться ни разу, если условие при первой же проверке выдаст «нет». Поэтому цикл с постусловием можно заменить циклом с предусловием, а наоборот — нет.
■ Пример 7. Записать алгоритм примера 6 с помощью цикла «до».
Решение.
ЦИКЛ С ПАРАМЕТРОМ (ЦИКЛ СО СЧЕТЧИКОМ, ИЛИ ЦИКЛ «ДЛЯ»)
Эта структура предписывает повторять команды тела цикла для всех значений некоторой переменной (параметра, или счетчика цикла).

Имя параметра цикла (счетчика) указывают в заголовке после служебного слова для. Затем с помощью служебных слов от и до задают начальное и конечное значение этого параметра.
Работа цикла «для» начинается с присвоения параметру начального значения. Если оно не превышает конечного значения, выполняются команды тела цикла. Затем значение параметра цикла увеличивается на единицу. Если оно снова не превышает конечного значения, опять происходит выполнение тела цикла. Если же полученное значение параметра превысит конечное, цикл будет завершен и управление передано следующей за циклом команде.
Цикл со счетчиком всегда выполняется i1 – i2 + 1 раз.
■ Пример 8. Записать алгоритм вычисления факториала числа N.
Решение. Факториал числа вычисляется по формуле N! = 1 × 2 × … × N. Следовательно, для расчета факториала надо организовать цикл со счетчиком, в котором перемножить последовательные целые числа от 2 до N. Значение 1!, равное 1, можно присвоить результирующей переменной до цикла.
Таблицы и массивы
Табличный способ организации данных позволяет удобно обрабатывать наборы однотипных данных. В языках программирования наборы табличных данных принято называть массивами. В алгоритмическом языке используют название «таблица».
■ Массив — конечный набор пронумерованных однотипных данных, имеющий имя.
Величины, которые входят в массив, называются его элементами. Количество элементов массива называется его размерностью.
На практике чаще всего используют массивы, содержащие числовые или литерные (символьные, текстовые) данные. Важным является требование однотипности данных.
Имя массива (таблицы) относится ко всему набору данных. Элементы массива различают по порядковому номеру, который называется индексом. Для обращения к элементу его индекс указывают в квадратных скобках сразу вслед за именем массива. Например, если массив имеет имя D, то третий его элемент обозначается D[3]. Такие имена называются индексированными именами. Индексы могут быть не только константами, но и переменными или целочисленными выражениями: D[j], D[k+1].
Различают одномерные и многомерные массивы.
Одномерный, или линейный массив представляет собой последовательность нумерованных по порядку элементов. Одномерные таблицы называют иногда векторами. В них всегда только одна строка или один столбец.
В одномерных таблицах или массивах могут быть записаны данные, относящиеся только к какому–либо одному факту. Например, результаты соревнований спортсменов по одному виду спорта, или регулярные показания температуры в одной местности, или оценки учащихся по одному предмету, или названия альбомов одного исполнителя.
Одномерная таблица, содержащая расстояния от Солнца до планет Солнечной системы (в астрономических единицах), может выглядеть как табличная строка:
Названия планет в этой таблице отсутствуют (иначе они бы образовали вторую строку). Чтобы узнать расстояние от Солнца до Марса, надо обратиться к четвертому элементу этой таблицы. Если, например, в программе такой массив расстояний от Солнца был поименован как Dist, то для обращения к 4–му элементу массива надо указать Dist[4].
Многомерные таблицы и массивы могут содержать данные о нескольких фактах — например, результаты соревнований спортсменов в нескольких видах спорта; измерения температуры, давления и влажности в разные месяцы в разных городах; оценки разных учащихся по разным предметам в разные дни; названия альбомов исполнителей, выпущенных в разные годы.
В отличие от индексированных элементов массива обычные переменные иногда называют скалярными.
Для описания таблицы в алгоритмическом языке используется служебное слово таб. Необходимо указать по порядку: тип элементов таблицы, служебное слово таб, имя таблицы, а затем в квадратных скобках через двоеточие начальный и конечный номера элементов таблицы.
Общий вид описания таблицы:тип элементов таб имя таблицы [наименьший индекс : наибольший индекс]
Например, для описания таблицы расстояний от Солнца необходимо учесть, что в ней содержатся нецелые числа, следовательно, тип данных таблицы — вещественный, и количество элементов равно 9:вещ таб Dist[1:9]
Для присвоения значений элементам таблицы (массива) используют операторы присваивания или процедуру ввода данных, как и для обычных переменных.
Например, присвоение значений элементам таблицы Dist можно описать на алгоритмическом языке следующим образом:
Зачастую ввод данных в массив или задачи их обработки связаны с перебором элементов массива. Для этих целей обычно используют циклы с параметром (со счетчиком). В теле цикла индекс массива обозначают переменной, и эта же переменная выступает в роли параметра (счетчика) цикла. Для параметра в заголовке цикла указывают перечень значений индекса массива. Например, если необходимо обработать все 20 значений массива Т, то следует записать цикл нц для i от 1 до 20 … кц и в теле цикла задать обработку для элемента T[i].
■ Пример 10. По данным о территории некоторых стран Европы (см. первую строку примера многомерной таблицы) рассчитать суммарную площадь этих стран.
Решение. В алгоритме необходимо предусмотреть ввод вещественных данных в таблицу (например, Terr) из 9 элементов. Для будущего суммарного результата необходимо отвести переменную (например, S), первоначально присвоить этой переменной нулевое значение. Затем организовать цикл с параметром, изменяющимся от 1 до 9 (количество элементов в таблице) и поочередно сложить предыдущее значение S с очередным элементом таблицы Terr[i]. Завершить алгоритм выводом результата.

Конспект урока по информатике «Алгоритмические конструкции».
Вернуться к Списку конспектов по информатике.
