Диаграммы, планы, карты
Ключевые слова: чертежи, масштаб, планы, карты, графики, гистограмма, круговая диаграмма, кольцевые диаграммы, точечная диаграмма, схема, диаграмма Венна, круги Эйлера, граф, дерево, интеллект-карты.
Код ОГЭ по информатике: 2.5.2. Диаграммы, планы, карты.
Графический способ представления информации позволяет в наглядной форме отобразить многие зависимости между данными, оценить величины, помогает решать задачи, принимать решения. К графическим средствам можно отнести карты и планы, схемы и чертежи, различного вида графики и диаграммы и др.
Чертежи — контурные изображения различных объектов. К чертежам, используемым в конструкторской деятельности, предъявляются определенные требования по их оформлению. В них, как правило, используются проекции объектов, созданные по правилам начертательной геометрии.
Отношение размеров изображения объекта на чертеже к их натуральной величине называется масштабом.
Изображение земной поверхности на плоскости в условных знаках, имеющее масштаб 1:10000 или крупнее, обычно называют планом (зачастую это топографические планы). Так же называется вид сверху или горизонтальный разрез какого–либо сооружения или предмета. Как правило, план выполняют в крупном масштабе.
Планы зданий, городов, местности помогают ориентироваться и легче воспринимать весь объект в целом.
Электронные карты предназначены для визуализации чертежей неба, земли, моря. Существуют топографические, геологические, метеорологические, морские карты, карты полезных ископаемых, звездного неба, автомобильных дорог и проч.
Для отображения информации на картах используют систему условных обозначений, которая включает специальные символы, цветовые поля, различные шрифты и т. п. Условные обозначения с их разъяснением располагают рядом с основным изображением карты и называют легендой. Там же указывают и масштаб карты.
Электронные карты могут быть представлены в виде отдельных графических файлов или лежать в основе работы специальных приложений (программ). Такие программы могут осуществлять масштабирование, поиск по карте, измерение расстояний, прокладку маршрутов и многое другое. Поисково–информационные картографические сервисы в Интернете позволяют осуществлять эти и другие операции в режиме онлайн.
Зачастую необходимо наглядно отобразить зависимость какой–либо величины от другой. С этой целью используют графики.
Графики — это одна из разновидностей диаграмм. В общем случае диаграмма — это геометрическое представление данных, показывающее их соотношение и выполненное в символьном виде одним из способов визуализации. Диаграммы в основном состоят из геометрических объектов (точек, линий, фигур различной формы и цвета) и вспомогательных элементов (осей координат, условных обозначений, заголовков и т. п.). Существуют тысячи разновидностей диаграмм. В большинстве случаев каждый вид диаграмм можно представить в двумерном (плоскостном) и трехмерном (объемном, пространственном) виде.
Диаграммы позволяют сопоставлять величины, наглядно отображать их изменения во времени, зависимости. Множество разновидностей диаграмм позволяют визуально подчеркнуть какие–либо конкретные особенности отображаемых данных.
Так, графики используют, если надо отобразить математическую зависимость величин друг от друга. Очень часто их применяют, чтобы показать тенденцию изменения данных во времени (или сравнить тенденции изменений сразу нескольких рядов данных). Обычно графики имеют равномерную шкалу.
Столбчатые (столбиковые) и линейчатые (ленточные, полосковые) диаграммы представляют величины данных в виде площадей прямоугольников — соответственно вертикальных или горизонтальных. Столбчатые диаграммы называют гистограммами. Обычно ширина всех их прямоугольников одинакова, а значение величин отображается их высотой.
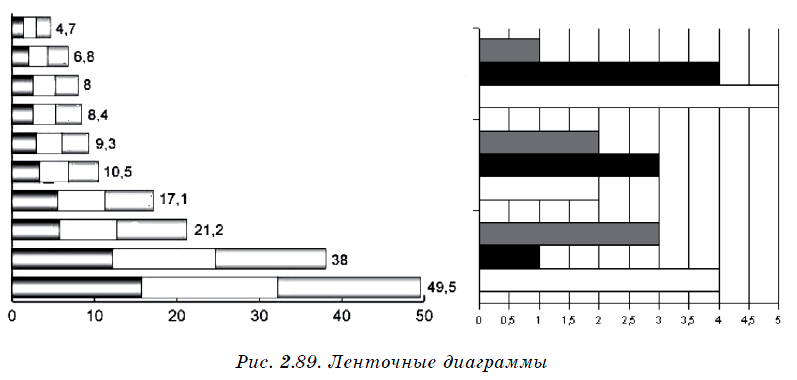
Ленточные диаграммы отличаются лишь горизонтальным расположением прямоугольников данных. Обе разновидности диаграмм удобны для демонстрации изменений величины. Часто они используются для сравнения между собой нескольких рядов данных. Иногда вместо прямоугольников в таких диаграммах используют конусы, цилиндры и другие геометрические объекты.
Также широко используются круговые диаграммы. Круг представляет всю совокупность данных, а каждый его сектор — относительную величину каждого значения. Эти диаграммы удобны, когда нужно показать долю каждой величины в общей совокупности, а особенно — подчеркнуть вклад какой–либо конкретной составляющей.
Кольцевые диаграммы содержат несколько колец — каждое кольцо представляет один ряд данных.
Точечная диаграмма (диаграмма рассеяния) изображает значения двух величин в виде точек на плоскости. Обычно значения независимого параметра откладывают по горизонтальной оси, а значения зависимого — по вертикальной. Точечные диаграммы используют для демонстрации наличия или отсутствия связи между двумя величинами.
Изображение системы, составных частей какого–либо объекта или процесса, их взаимосвязи называется схемой. Как правило, такое изображение представляет объект в самых общих чертах. Например, схема двигателя может упрощенно представлять принцип его функционирования, схема химической реакции дает общее представление о природе участвующих в ней элементов и соединений. Блок–схема алгоритма помогает изложить его основные этапы.
Схематическое представление данных также можно реализовать в виде диаграмм. Например, диаграммы Венна схематично изображают в виде пересекающихся кругов все возможные отношения нескольких множеств данных.
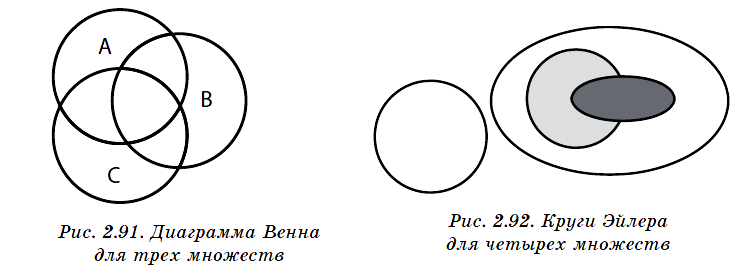
Каждый круг изображает совокупность элементов одного из множеств. Если какие–либо элементы принадлежат сразу нескольким множествам, им соответствует пересечение кругов, представляющих эти множества. Если на схеме указываются не все возможные пересечения подмножеств, то такое отображение называется кругами Эйлера.
Граф — это схема, отображающая объекты в виде точек, а связи между ними в виде линий, соединяющих эти точки. Точки называются вершинами (или узлами) графа, соединяющие линии — дугами (или ребрами) графа.
Последовательность дуг и соединенных ими промежуточных вершин — путь между вершинами графа. Если у отрезков пути заданы направления (в виде стрелок), такой граф называют ориентированным, или направленным.
С помощью графов отображают маршруты движения пассажиров, перевозки грузов, транспортировки энергетических ресурсов, компьютерные сети. Графы применяют при составлении расписаний транспорта, занятий, соревнований, при анализе и проектировании систем электро–, водо–, газо–, теплоснабжения, для распределения радиочастот сотовой связи с целью достижения максимальной пропускной способности каналов.
Графы помогают определить маршруты следования информации в компьютерных сетях (организовать маршрутизацию). Графами являются схемы метрополитенов, структурные схемы молекул, сетевые графики строительства: в них вершинами являются строительные работы, а дугами — связи между ними. Блок-схема алгоритма — это тоже граф, вершинами которого служат функциональные блоки, а дуги (линии) определяют очередность выполнения блоков.
Графы очень часто используются при решении логических и иных задач.
Иерархию (подчиненность) объектов отображают в графическом виде с помощью деревьев. Дерево — граф, в котором две любые вершины соединены только одним путем и нет циклов (нельзя из вершины пройти по нескольким различным ребрам и вернуться в ту же вершину).
Название этой схемы связано с тем, что она напоминает перевернутое дерево. Самую верхнюю вершину дерева (не имеющую родительской для нее вершины) называют корнем дерева. Линии, связывающие элементы дерева, называются ветвями, сами элементы называются узлами. Узлы без потомков называются конечными узлами или листьями. Структуры деревьев похожи на генеалогические деревья, поэтому для отношений между узлами дерева используют названия «родители» и «потомки» (родительские и дочерние узлы).
Многие структуры могут быть представлены в виде деревьев. Например, структура файловых папок в операционной системе, поисковые каталоги в Интернете.
Деревья — очень удобный инструмент представления информации. Благодаря тому что при обходе дерева невозможны циклы (повторы) в пути, эту форму используют для организации данных в алгоритмах.
В виде древовидного изображения реализуются и интеллект-карты — схемы, отображающие процесс мышления человека. Эти схемы имеют множество названий — их называют также картами разума, картами памяти, когнитивными картами, mind map (англ. карты ума), ассоциативными картами, диаграммами связей. Они помогают показать взаимоотношения некоторой идеи или понятия и связанной с ней ассоциативно информацией.
Для этого в центре схемы размещают ключевое понятие, а радиально вокруг него — в произвольном порядке связанные с ним по смыслу иные понятия –единичные или сгруппированные в виде ветвей. Такой способ записи позволяет диаграмме неограниченно расти и дополняться.
Используются интеллект–карты для представления идей, их классификации, для наглядности в обучении, для решения задач, принятия решений, способствуют зарождению новых идей.
Графическое представление данных значительно облегчает решение многих задач. Например, диаграммы Венна и круги Эйлера помогают решить задачи, где требуется определить или сравнить множества значений. Для этого надо каждое множество изобразить в виде соответствующего круга. Если множества имеют общие элементы, круги должны пересекаться, в ином случае — нет.
- Пример 1
Изображение было создано с использованием трех основных цветов модели RGB. Отобразить с помощью диаграмм Венна цветовой результат наложения элементов рисунка друг на друга.
Решение. Пусть каждый из трех кругов отображает множество элементов рисунка одного из основных цветов RGB — красного, зеленого и синего. Тогда пересечение этих кругов показывает элементы рисунка, окрашенные в результате смешения красного и зеленого (= желтый), зеленого и синего (= голубой), синего и красного (= фиолетовый) цветов, а также их всех трех вместе (= белый).
- Пример 2
Отобразить с помощью кругов Эйлера пересечение трех множеств жителей — области Область1, области Область2 и района второй области Район1.
Решение. Одно из множеств (жителей района) является подмножеством другого (жителей Области2) — следовательно, один из кругов будет полностью лежать внутри другого. Еще один круг не будет пересекаться с первыми двумя, поскольку множество жителей разных областей не имеют общих элементов.
Для решения задач, связанных с маршрутами, используют представление данных в виде графов. Например, если требуется отыскать маршруты между некоторыми пунктами, удобно отобразить имеющиеся сообщения между пунктами в виде графа. Затем в соответствии с направлением отрезков рассчитать пути передвижения. Для этого этапа можно использовать представление маршрутов в виде дерева. При этом корнем дерева надо выбрать конечный или начальный пункт (в зависимости от задачи) и присоединять к нему в виде вершин все доступные пункты. Затем те же операции проделать для всех последующих или только подходящих по условию вершин дерева. По построенному дереву можно будет рассчитать количество путей сообщения или выписать конкретный необходимый маршрут.
- Пример 3
На рисунке изображена схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город К?
Решение. Способ 1.
Граф всех возможных передвижений уже задан. Построим дерево решений задачи — всех маршрутов из А в К. Для этого изобразим город К как корень дерева. Соединим его со всеми городами, из которых можно попасть в К, — Ж, З, И.
К каждому из листьев дерева — Ж, З, И — присоединим вершины, отвечающие городам, откуда можно добраться до городов Ж, З, И. Для вершины Ж — В, Д, Е. Для вершины З — Д. Для вершины И — Е.
Так продолжим до тех пор, пока в каждой ветви не будет достигнута вершина начала маршрута А. Подсчитаем количество листьев А в построенном дереве — это и будет количество путей от листьев до корня дерева (т. е. от города А до К).
Таких листьев 13.
Решение. Способ 2.
Эту задачу можно решить и без использования дерева, но с большим количеством подсчетов. Обозначим через NH количество различных путей из А в М, где М — любой из заданных городов. Начнем подсчет количества путей в А с конца маршрута — от города К. В город К можно приехать из городов Ж, З, И. Следовательно, количество путей в А будет равно сумме путей в каждый из этих трех городов:
х = NЖ + NЗ + NИ
Аналогично подсчитаем количество путей в каждый из трех городов Ж, З, И:
NЖ = NВ + NД + NE
NЗ = NД; NИ = NЕ
Продолжим подсчеты до тех пор, пока не будет достигнут город А в каждом из маршрутов.
NВ = NА + NБ + NГ
NД = NБ + NЕ
NЕ = NГ
Учтем, что NА = 1: NБ = NА = 1; NГ = NА = 1. Тогда предыдущие выражения примут вид:
NB = 1 + 1 + 1 = 3
NД = 1 + 3 = 4
NЕ = 1
Подставим найденные величины в начальные выражения:
NЖ = 3 + 4 + 1 = 8
N3 = 4; NИ = 1
х = NЖ + N3 + NИ = 8 + 4 + 1 = 13
Ответ: 13.
Конспект урока по информатике «Диаграммы, планы, карты».
Вернуться к Списку конспектов по информатике.