Опорный конспект 1. Окружности
Наглядная геометрия 9 класс. Опорный конспект 1. Окружности
На плоскости прямая может не иметь с окружностью общих точек, может иметь с ней одну общую точку — в этом случае она называется касательной, и может пересекать окружность в двух точках — такая прямая называется секущей. Других вариантов взаимного расположения прямой и окружности нет. Вариантов взаимного расположения двух окружностей больше — 5, поскольку одна из окружностей может располагаться как снаружи, так и внутри другой окружности.
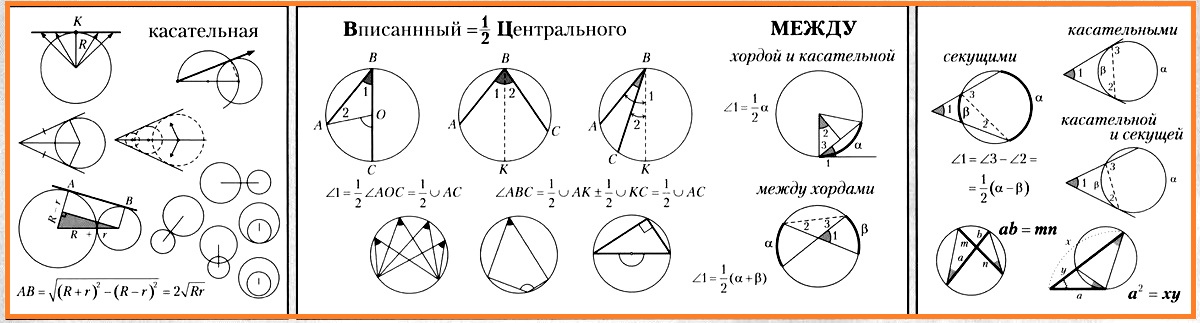
Углы, связанные с окружностью, имеют определенные названия. Угол с вершиной в центре окружности называется центральным углом. Угол, вершина которого лежит на окружности, а стороны пересекают окружность, называется вписанным. Оказывается, что вписанный угол равен 1/2 соответствующего центрального угла.
В этом конспекте мы узнаем, что дуга окружности может измеряться в градусах. Мы научимся вычислять угол между пересекающимися хордами, между секущими, между касательной и хордой, имеющими общую точку. Еще мы выясним, как связаны отрезки пересекающихся хорд, а также отрезок касательной и отрезки секущей, проведенных из одной точки к окружности.
ТАБЛИЦА «Окружности»

1. Касательная. Свойство касательной.
Касательной называется прямая, которая имеет единственную общую точку с окружностью.
Теорема (свойство касательной). Радиус, проведенный в точку касания, перпендикулярен касательной.
Доказательство. Дана касательная. Она имеет единственную общую точку с окружностью. Другие точки прямой лежат вне окружности и поэтому дальше от центра (расстояние до них больше радиуса). Значит, длина радиуса, проведенного в точку касания, — это КРАТЧАЙШЕЕ расстояние от центра до касательной. А кратчайшее расстояние измеряется длиной перпендикуляра.
2. Признак касательной.
Теорема (признак касательной). Прямая, перпендикулярная радиусу в конечной его точке на окружности, является касательной.
Доказательство. (Все рассуждения проводятся как в предыдущей теореме, только в обратном порядке.)
Радиус перпендикулярен к прямой (она еще не касательная!). Длина перпендикуляра — это КРАТЧАЙШЕЕ расстояние от центра до прямой. Значит, другие точки прямой лежат дальше от центра. Так как расстояние до них больше радиуса, то все они лежат вне окружности и прямая имеет единственную общую точку с окружностью. А такая прямая является касательной.
3. Построение касательной циркулем и линейкой.
Построение касательной циркулем и линейкой. Соединяем данную точку с центром окружности. На полученном отрезке как на диаметре строим окружность, которая пересекает данную. Через данную точку и точку пересечения окружностей проводим прямую, которая и будет касательной.
Доказательство. Так как угол с вершиной на окружности, опирающийся на диаметр, — прямой (доказано нами в 7 классе), то построенная прямая проходит через точку на окружности перпендикулярно радиусу, проведенному в эту точку. Она является касательной по признаку касательной.
Исследование. Из данной точки вне окружности можно провести две касательных. Задача имеет два решения.
4. Свойство касательных, проведенных из одной точки к окружности.
Теорема. Отрезки касательных, проведенных из одной точки к окружности, равны между собой.
Доказательство. Соединим данную точку с центром окружности. Радиусы, проведенные в точки касания, перпендикулярны касательным. Прямоугольные треугольники равны по катету и общей гипотенузе. Отсюда следует равенство отрезков касательных.
5. Свойство окружностей, вписанных в угол.
Теорема. Центр окружности, вписанной в угол, лежит на биссектрисе угла.
Доказательство. Опустив радиусы в точки касания, получим, что центр окружности равноудален от сторон угла. А биссектриса — это геометрическое место точек, равноудаленных от сторон угла (доказано нами в 7 классе).
6. Взаимное расположение двух окружностей.
R и r — радиусы окружностей, d — расстояние между ними. 1) d > R + r — окружности не пересекаются и расположены внешним образом; 2) d = R + r — касаются внешним образом — одна общая точка; 3) R – r < d < R + r — пересекаются; 4) d = R – r — касаются внутренним образом; 5) d < R – r — не пересекаются и одна расположена внутри другой (концентрические — если центры совпадают).
7. Длина отрезка общей внешней касательной.
Задача. Окружности с радиусами R и r касаются внешним образом. Найти отрезок общей внешней касательной, заключенный между точками касания.
Решение. Проведем радиусы в точки касания. Они перпендикулярны касательной. Из центра меньшей окружности проведем прямую, параллельную касательной. Получим прямоугольник (три угла четырехугольника — прямые). Две его стороны равны радиусу меньшей окружности, две другие — искомому отрезку касательной. В прямоугольном треугольнике гипотенуза равна R + r, а катет равен R – r. Ho теореме Пифагора находим второй катет. Искомый отрезок![]()
8. Центральный угол. Градусная мера дуги. Вписанный угол.
Центральным называется угол с вершиной в центре окружности. Градусная мера центрального угла равна градусной мере дуги, на которую он опирается. (Иногда говорят просто: центральный угол равен дуге, на которую он опирается, имея в виду их градусные меры.) Полуокружность содержит 180°, окружность — 360°.
Вписанным называется угол, вершина которого лежит на окружности, а стороны пересекают окружность. Центральный и вписанный углы соответствующие, если они опираются на одну и ту же дугу окружности, которая заключена внутри угла.
9. Свойство вписанного угла.
Теорема. Вписанный угол равен половине дуги, на которую он опирается, или половине соответствующего центрального угла.
Доказательство. Случай 1. Сторона вписанного угла проходит через диаметр. Угол АОС равен сумме углов 1 и 2 как внешний. Но ΔАОВ — равнобедренный (ОА = ОВ как радиусы). Поэтому углы 1 и 2 равны. Вписанный угол 1 равен половине центрального угла АОС, а значит, и половине дуги АС.
Случай 2. Стороны угла лежат по разные стороны от центра. Проведем диаметр ВК. Углы АВК и СВК равны половине дуг АК и СК. Угол АВС равен полусумме этих дуг, т. е. половине дуги АС.
Случай 3. Стороны угла лежат по одну сторону от центра. Проведем диаметр ВК. Углы АВК и СВК равны половине дуг АК и СК. Угол АВС равен полуразности этих дуг, т. е. половине дуги АС.
10. Вписанные углы, опирающиеся на одну и ту же дугу.
Следствие 1. Вписанные углы, опирающиеся на одну и ту же дугу, равны.
Доказательство. Каждый из этих углов равен половине их общей дуги.
11. Вписанный угол, опирающийся на диаметр.
Следствие 2. Вписанный угол, опирающийся на диаметр, — прямой, и, наоборот, если вписанный угол прямой, то он опирается на диаметр.
Доказательство. Если вписанный угол опирается на диаметр, то соответствующий центральный угол — развернутый, а вписанный угол равен его половине, т. е. 90°.
Если вписанный угол — прямой, то соответствующий центральный угол равен 180°, т. е. он — развернутый. Поэтому прямой вписанный угол опирается на диаметр.
12. Угол между касательной и хордой.
Теорема. Угол между касательной и хордой равен половине дуги, заключенной внутри угла.
Доказательство. ∠1 и ∠2 дополняют ∠3 до 90°. Поэтому ∠1 = ∠2, a ∠2 равен половине центрального угла, т. е. половине дуги а.
13. Угол между двумя пересекающимися хордами.
Теорема. Угол между пересекающимися хордами равен полусумме дуг, заключенных внутри данного и внутри вертикального ему угла.
Доказательство. Соединим концы хорд. ∠1 — внешний. Тогда![]()
14. Угол: а) между двумя секущими, б) между касательной и секущей,
в) между двумя касательными.
Теорема. Угол между двумя секущими, проходящими через одну точку вне окружности, равен полуразности дуг, заключенных внутри угла.
Доказательство. Соединим первую точку пересечения первой секущей и окружности со второй точкой пересечения второй секущей и окружности. ∠3 = ∠1 + ∠2 как внешний. Тогда![]()
Доказательство не изменится, если секущая займет крайнее положение касательной. Поэтому
- угол между касательной и секущей равен полуразности дуг, заключенных внутри угла,
- угол между касательными равен полуразности дуг, заключенных внутри угла.
15. Свойство отрезков пересекающихся хорд.
Теорема. Произведения отрезков пересекающихся хорд равны между собой.
Доказательство. Соединим концы хорд. Из подобия треугольников по двум углам (равны вертикальные углы и равны вписанные углы, опирающиеся на одну и ту же дугу) следует: a/n = m/b, ab = mn.
16. Свойство касательной и секущей, проведенных из одной точки к окружности.
Теорема. Квадрат отрезка касательной равен произведению всего отрезка секущей на его внешнюю часть.
Доказательство. Треугольники со сторонами а, x и а, у подобны по двум углам (один угол общий и закрашенные углы измеряются половиной своей дуги). Из подобия следует, что a/y = x/a, а2 = ху.
Следствие. Для всех секущих, проведенных из одной точки, произведения всего отрезка секущей на его внешнюю часть равны между собой. (Все произведения равны квадрату отрезка общей касательной, проведенной из той же точки.)
ЭТО НУЖНО ЗНАТЬ !

Это конспект по геометрии в 9 классе «Опорный конспект 1. Окружности». Выберите дальнейшие действия:
