Поурочное планирование по геометрии для 8 класса. Ориентировано на работу с УМК Атанасян и др. Геометрия 8 класс. Глава VII. ПОДОБНЫЕ ТРЕУГОЛЬНИКИ. Урок 36 Решение задач на применение признаков подобия треугольников. Вернуться к Списку уроков Тематического планирования.

Урок 36. Решение задач на применение
признаков подобия треугольников

Основные дидактические цели урока: сформировать у учащихся навыки применения признаков подобия треугольников при решении задач; совершенствовать навыки доказательств теорем.

Ход урока

I. Организационный момент.

Мотивация к учебной деятельности. (Учитель сообщает тему урока, формулирует цели урока.)

II. Актуализация знаний учащихся

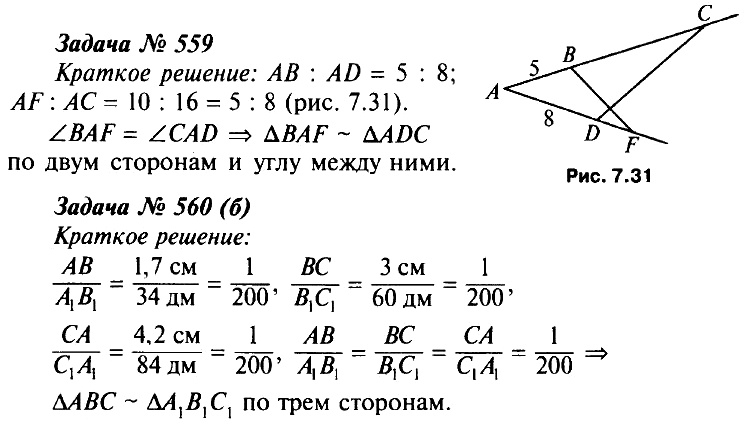
1. Проверка домашнего задания. (Учитель проверяет решение задач № 559, 560 (б). Два ученика заранее готовят решение на доске.)

2. Теоретический опрос. (Два ученика готовят доказательства теорем у доски.)

• Сформулируйте признаки подобия треугольников.
• Докажите теоремы, выражающие второй и третий признаки подобия треугольников.

3. Работа по индивидуальным карточкам. (3—6 учеников работают по карточкам во время теоретического опроса.)

I уровень сложности

Подобны ли треугольники АВС и А₁В₁С₁, если известно, что:

1. АВ = 10 см; ВС = 5 см; АС = 7 см; А₁В₁ = 15 см; В₁С₁ = 7,5 см; A₁С₁ = 9,5 см?
2. ∠A = 37°, ∠B = 48°, ∠C₁ = 95°, ∠B₁ = 48°?
3. АВ = 10 см, ВС = 8 см, А₁В₁ = 5 см, А₁С₁ = 3 см, ∠C = ∠C₁ = 90°?

II уровень сложности

1. Прямая, параллельная стороне MN треугольника MNK, пересекает стороны КМ и KN в точках Е и F соответственно, КЕ = 6 см, KM = 10 см, KF = 9 см, KN = 15 см. Найдите отношения. a) EF: MN, б) P_KMN : Р_КЕF, в) S_KEF : S_KMN.
2. Точка Е — середина стороны AD параллелограмма ABCD. В каком отношении прямая BE делит диагональ АС параллелограмма? Найдите отношение площади треугольника АВЕ и четырехугольника BCDE.

III уровень сложности

1. Основания трапеции равны 9 и 6 см, а высота равна 10 см. Найдите разность расстояний от точки пересечения диагоналей трапеции до ее оснований.
2. Докажите признак подобия прямоугольных треугольников по гипотенузе и катету.
3. Решение задач по готовым чертежам.

• 1) Рис. 7.32. Найти: ∠C₁,  В₁С₁.
• 2) Рис. 7.33. Найти: ∠C, ∠C₁
• 3) Рис. 7.34. Найти: ВМ.
• 4) Рис. 7.35. Найти: ВС.
• 5) Рис. 7.36. Найти: ∠DCA.
• 6) Рис. 7.37. Найти АВ, NC.

Ответы к задачам по готовым чертежам:

• 1) ∠C₁ = 71°, В₁С₁ = 15 см.
• 2) ∠C = ∠C₁ = 60°.
• 3) ВМ = 6 см.
• 4) BC = 20/3.
• 5) Обратите внимание! Ответ автора задания ∠DCA = 90°. Однако, этот ответ нельзя признать правильным в виду каких-то опечаток в рис.7.36. Единственный вывод из рисунка: треугольники ABC и АCD подобны (по трем сторонам), но в таком случае ответ должен быть 80°, а не 90°. Но самый противоречивый момент связан с тем, что треугольники с заявленными сторонами и углами не существуют. Если считать, что стороны на рисунке указаны правильно, то вместо 80° должно быть указано 92,73°, а вместо 55° должно быть 45,52°. Тогда правильный ответ будет ∠DCA =  92,73°.
• 6) АВ = 8, NC= 8.

(После окончания самостоятельного решения задач и самопроверки по готовым ответам выполняется самооценка.) Критерии оценивания:

• оценка «5» — правильно решены пять-шесть задачи;
• оценка «4» — правильно решены четыре задачи;
• оценка «3» — правильно решены две-три задачи;
• оценка «2» — не ставится.

(Учащиеся, справившиеся со всеми задачами, решают дополнительные задачи.)

Дополнительные задачи

1. Диагональ АС трапеции ABCD (АВ||CD) делит ее на два подобных треугольника. Найдите площадь трапеции ABCD, если АВ = 25 см, ВС = 20 см, АС = 15 см.

Ответ: S_ABCD = 204 см².

2. Угол В треугольника AВС в два раза больше угла А. Биссектриса угла В делит сторону АС на части AD = 6 см и CD = 3 см. Найдите стороны треугольника АВС.

Ответ: АС = 9 см, АВ = 6√3 см, ВС = 3√3 см.

III. Самостоятельная работа

I уровень сложности

Вариант 1

1. Рис. 7.38. Доказать: ΔАВС ~ ΔА₁В₁С₁
2. Продолжения боковых сторон трапеции ABCD пересекаются в точке О. Найдите ВО и отношение площадей треугольников ВОС и AOD, AD = 5 см, ВС = 2 см, АО = 25 см.

Вариант 2

1. Рис. 7.39. Доказать: ΔАВС ~ ΔА₁B₁С₁.
2. АВ и CD пересекаются в точке О, АО = 12 см, ВО = 4 см, СО = 30 см, DO = 10 см. Найдите угол САО, если ∠DBO = 61°. Найдите отношение площадей треугольников АОС и BOD.

II уровень сложности

Вариант 1.

1. Рис. 7.40. Доказать: ΔАВС ~ ΔА₁В₁С₁
2. Прямая, параллельная стороне АС треугольника АВС, пересекает стороны АВ и ВС соответственно в точках М и Н. Найдите АС и отношение площадей треугольников АВС и ВМН, если МВ = 14 см, АВ = 16 см, МН = 28 см.

Вариант 2

1. Рис. 7.41. Доказать: ΔМВН ~ ΔСВA.
2. В треугольнике АВС АВ = 15 м, АС = 20 м, ВС = 32 м. На стороне АВ отложен отрезок AD = 9 м, а на стороне АС — отрезок АЕ = 12 м. Найдите DE и отношение площадей треугольников АВС и ADE.

III уровень сложности

Вариант 1

1. Дано: ∠1 = ∠2, AD = 4, АС = 9 (рис. 7.42). Найти: АВ, S_ABD : S_ABC.
2. Диагонали четырехугольника ABCD пересекаются в точке О, АО • ВО = СО • DO. Докажите, что площади треугольников ACD и ABD равны.

Вариант 2

1. Дано: ВС ⊥ АС, МН ⊥ ВС, 2МС = ВС, МН = 0,5АС (рис. 7.43). Доказать: АВ||СН. Найти. S_АВС : S_MCH.
2. В трапеции ABCD AD и ВС — основания, О — точка пересечения диагоналей, АО : ОС = 3 : 2. Найдите отношение площадей треугольников АВС и ACD.

(Ответы на самостоятельную работу смотрите в уроке 37)

IV. Рефлексия учебной деятельности

1. Сформулируйте признаки подобия треугольников.
2. В каком случае подобны равносторонние, равнобедренные, прямоугольные треугольники?

Домашнее задание. Решить задачи № 562, 563, 604, 605.

Вы смотрели: Поурочное планирование по геометрии для 8 класса. УМК Атанасян и др. (Просвещение). Глава VII. ПОДОБНЫЕ ТРЕУГОЛЬНИКИ. Урок 36 Решение задач на применение признаков подобия треугольников.

Вернуться к Списку уроков Тематического планирования.