Множества. Операции над множествами

Ключевые слова конспекта: множества, операции над множествами, подмножество, пересечение множеств, объединение множеств, элемент множества, числовые множества, обозначение некоторых числовых множеств.

В жизни часто приходится встречаться с различными совокупностями объектов, объединёнными в одно целое по некоторому признаку. Для обозначения этих совокупностей используются различные слова. Например, говорят: «стадо коров», «букет цветов», «команда футболистов» и т. д.

В математике в целях единообразия для обозначения совокупностей употребляется единый термин — множество. Например, говорят: множество чётных чисел, множество двузначных чисел, множество правильных дробей со знаменателем 5.

Термин «множество» употребляется и тогда, когда речь идёт о нечисловых множествах. Например, говорят о множестве диагоналей многоугольника, о множестве точек координатной плоскости, о множестве прямых, проходящих через данную точку.

Объекты или предметы, составляющие множество, называют элементами множества. Например, число 89 — элемент мнoжества двузначных чисел; точка В — элемент мнoжества вершин многоугольника ABCDE.

Множeства бывают конечные и бесконечные. Например, множество двузначных чисел — конечное множество (оно содержит 90 элементов), а множество чётных чисел — бесконечное множество.

Конечное мнoжество может содержать миллиард элементов, 2 элемента, 1 элемент или даже не содержать ни одного элемента.

Пустое множeство — это мнoжество, не содержащее ни одного элемента. Для обозначения пустого мнoжества ввели специальный знак ∅.

Конечные множeства обычно записывают с помощью фигурных скобок. Например, множество вершин пятиугольника ABCDE можно записать так:  {А, В, С, D, Е},  а множество двузначных чисел, кратных 15, так: {15, 30, 45, 60, 75, 90}.  В таких случаях говорят, что множество задано перечислением его элементов.

Множeства принято обозначать большими буквами латинского алфавита. Например, рассмотренные выше множества вершин пятиугольника и двузначных чисел, кратных 15, можно обозначить соответственно буквами К и L и записать так: К = {А, В, С, D, Е};  L = {15, 30, 45, 60, 75, 90}.

Для основных числовых множеств введены специальные обозначения: множество натуральных чисел обозначают буквой N (от латинского слова natural — «естественный»), множество целых чисел — буквой Z (от немецкого слова zahl — «число»), множество рациональных чисел — буквой Q (от латинского слова quotient — «отношение»).

Число -8 является элементом мнoжества Z. Иначе говорят, что число -8 принадлежит множеству Z. Это предложение записывают короче: -8 ∈ Z. Число 0,17 не принадлежит множеству N (не является элементом множества N). Для выражения этого факта принята следующая запись: 0,17 ∉ N.

В тех случаях, когда задание множества перечислением элементов невозможно (как для бесконечного множества) или громоздко (как для конечного мнoжества с большим числом элементов), множество задают описанием, указав его характеристическое свойство, т. е. свойство, которым обладают все элементы этого множeства и не обладают никакие другие объекты.

Зададим с помощью описания некоторые мнoжества.  Пусть А = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14}. Зададим это множество описанием, используя понятие характеристического свойства. Множeство А можно охарактеризовать как «множество всех натуральных чисел от 1 до 14 включительно», или как «множество всех натуральных чисел, меньших 15», или, используя знаки ∈ , < и букву х для произвольного элемента множества А, как «множество значений х, где х ∈ N и х < 15».

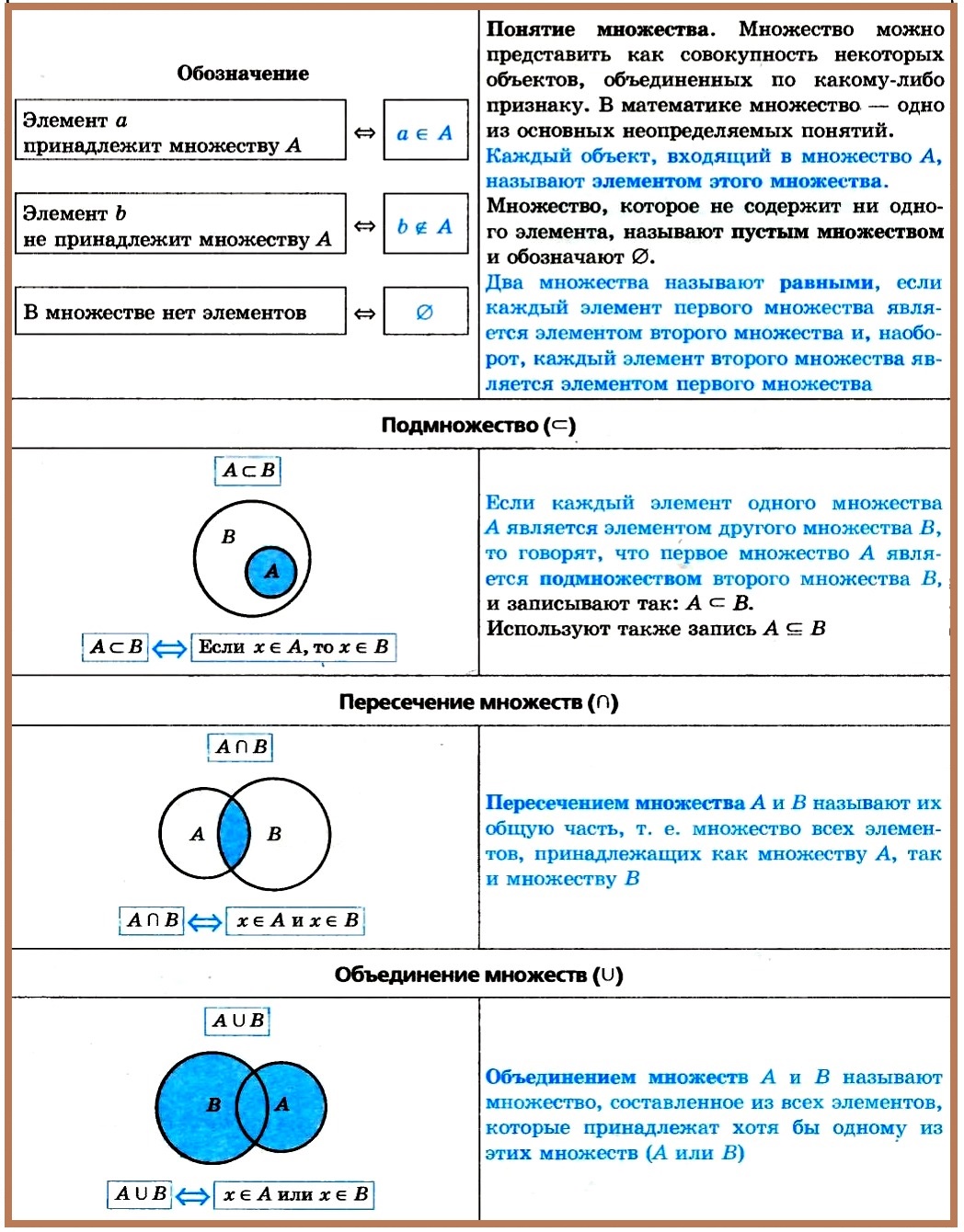
Операции над множествами

Числовые множества

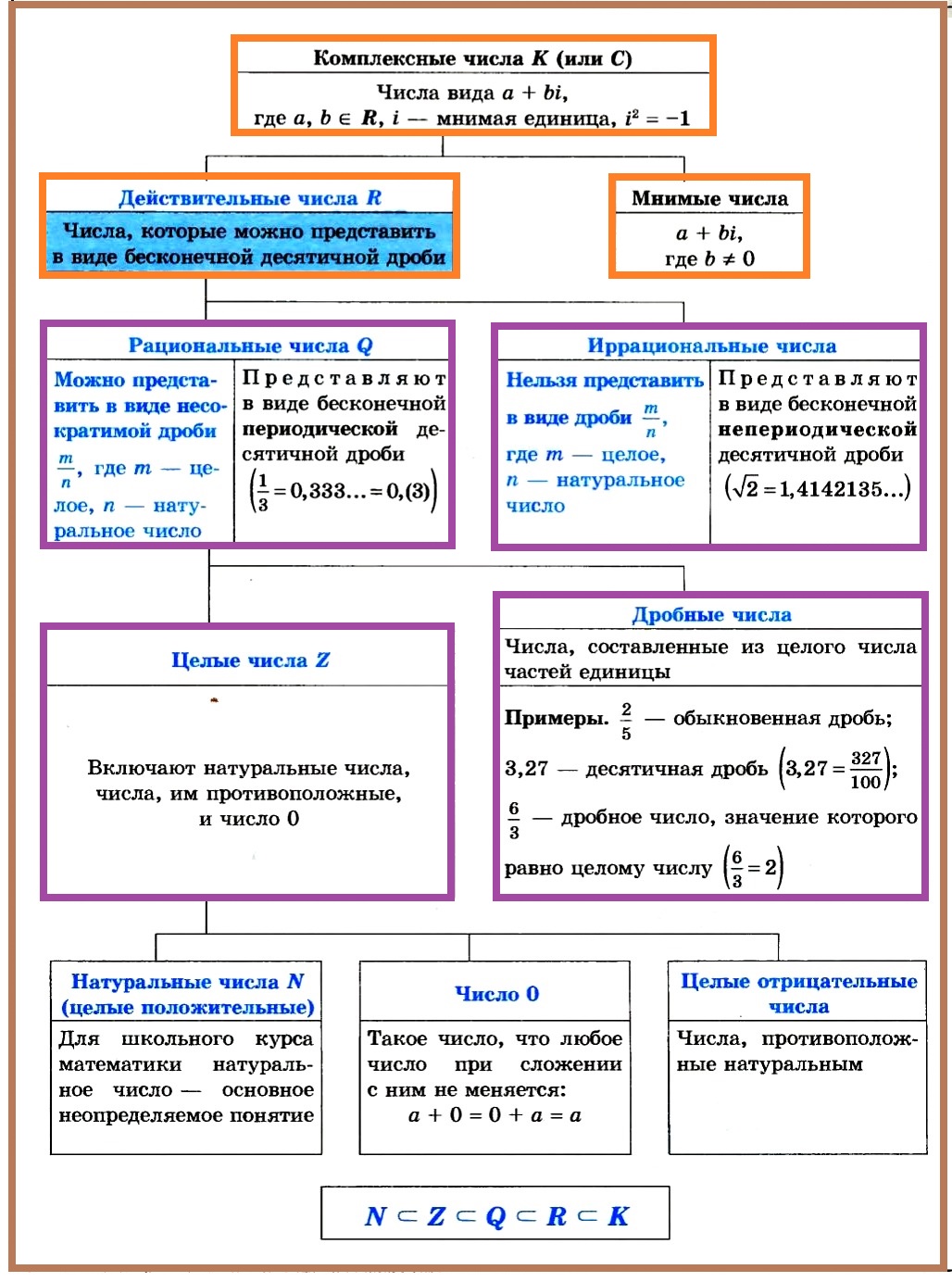
Обозначения некоторых числовых множеств

Это конспект по математике на тему «Множества. Операции над множествами». Выберите дальнейшие действия:

• Перейти к следующему конспекту: 
• Вернуться к списку конспектов по Математике.
• Проверить знания по Математике.