Прямоугольный треугольник

Ключевые слова: прямоугольный треугольник, свойства и признаки прямоугольного треугольника, метрические соотношения в прямоугольном треугольнике, признаки равенства и подобия.

Определение прямоугольного треугольника

Прямоугольный треугольник — треугольник, имеющий прямой угол. Стороны, образующие прямой угол, называют катетами, а сторону, противолежащую к прямому углу, называют гипотенузой.

Свойства прямоугольного треугольника

1. Катет меньше гипотенузы.
2. Квадрат гипотенузы равен сумме квадратов катетов (теорема Пифагора): с² = а² + b².
3. Сумма острых углов прямоугольного треугольника равна 90°.
4. Медиана, проведенная к гипотенузе, равна половине гипотенузы (радиусу окружности, описанной около треугольника).
5. Радиус окружности, вписанной в прямоугольный треугольник, можно вычислить по формуле: r = (a + b – c)/2.
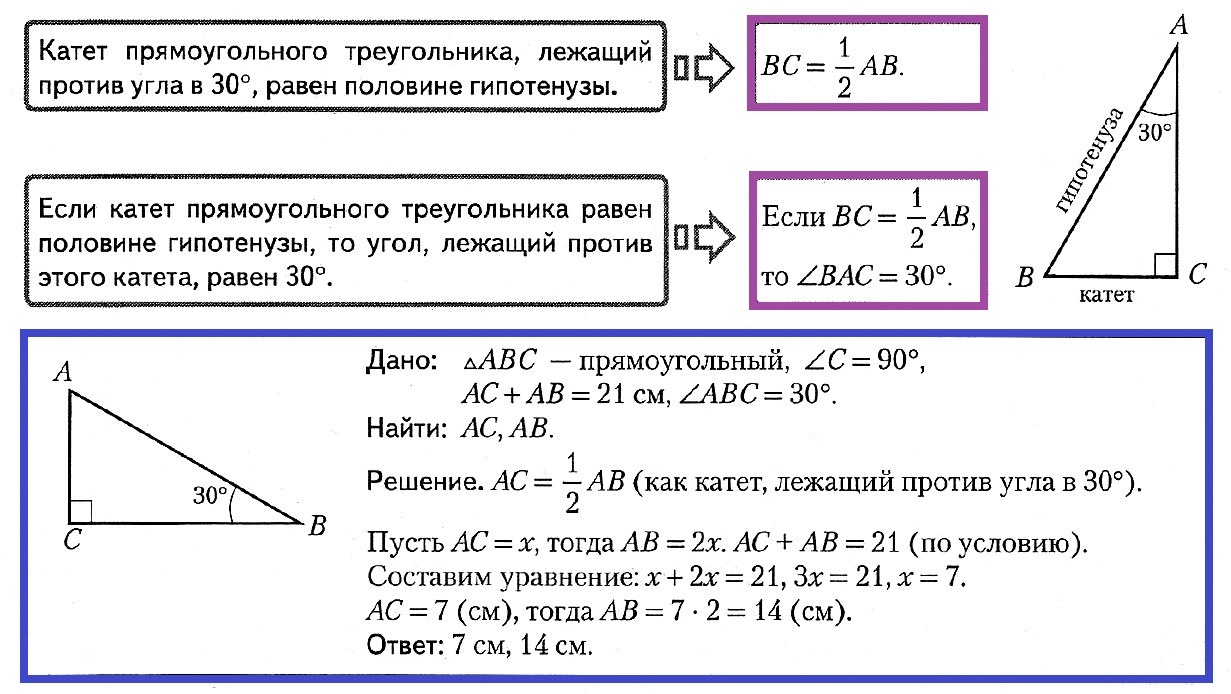
6. Катет прямоугольного треугольника, лежащий против угла в 30° (малый катет), равен половине гипотенузы.
7. Если катет прямоугольного треугольника равен 1/2 гипотенузы, то угол, лежащий против этого катета, равен 30°.
8. Катет прямоугольного треугольника, лежащий напротив угла в 60° (большой катет), равен малому катету этого треугольника, умноженному на √3.
9. В равнобедренном прямоугольном треугольнике гипотенуза равна катету, умноженному на √2.
10. Медиана прямоугольного треугольника, проведенная к его гипотенузе, делит треугольник на два равнобедренных треугольника, основаниями, которых являются катеты данного треугольника.

Признаки равенства прямоугольных треугольников

Два прямоугольных треугольника равны если:
• два катета одного треугольника равны двум катетам другого;
• катет и острый угол одного треугольника равны катету и острому углу другого треугольника;
• гипотенуза и острый угол одного треугольника равны гипотенузе и острому углу другого треугольника;
• гипотенуза и катет одного треугольника равны гипотенузе и катету другого треугольника.

Метрические соотношения
в прямоугольном треугольнике

Три равенства, которые называют метрическими соотношениями в прямоугольном треугольнике:

• Квадрат высоты прямоугольного треугольника, проведённой к гипотенузе, равен произведению проекций катетов на гипотенузу: h² = c_a • c_b.
• Квадрат катета равен произведению гипотенузы и проекции этого катета на гипотенузу: a² = c • c_a; b² = c • c_b.

ОПРЕДЕЛЕНИЕ.
Отрезки, на которые высота делит гипотенузу, называют проекциями катетов на гипотенузу.

h − высота прямоугольного треугольника. Часто проекции обозначают с помощью индексов. Например, запись c_a указывает на то, что это проекция катета a на гипотенузу c.

Теорема о высоте прямоугольного треугольника. Высота прямоугольного треугольника, проведённая к гипотенузе, делит треугольник на два подобных прямоугольных треугольника, каждый из которых подобен данному треугольнику.

Доказательство: 1) Пусть в прямоугольном треугольнику АСВ: ∠A = α, ∠B = β. Сумма этих углов равна α + β = 90°.
2) Высота CH делит треугольник ACB на два прямоугольных треугольника в каждом из которых есть угол α и угол β.
3) Следовательно, все три треугольника подобны по двум углам: △ACB ∼ △AHC ∼ △CHB.

Это конспект по теме «Прямоугольные треугольники». Выберите дальнейшие действия:

• Перейти к следующему конспекту: ЗАДАЧИ по теме Прямоугольные треугольники
• Вернуться к Списку конспектов по геометрии