
«Натуральные числа. Признаки делимости. НОД и НОК.»
Ключевые слова конспекта: Натуральные числа. Арифметические действия над натуральными числами. Делимость натуральных чисел. Простые и составные числа. Разложение натурального числа на простые множители. Признаки делимости на 2, 3, 5, 9, 4, 25, 10, 11. Наибольший общий делитель (НОД), а также наименьшее общее кратное (НОК). Деление с остатком.
Натуральные числа — это числа, которые используются для счета предметов — 1, 2, 3, 4, … Но число 0 не является натуральным!
Множество натуральных чисел обозначают N. Запись «3 ∈ N» означает, что число три принадлежит множеству натуральных чисел, а запись «0 ∉ N» означает, что число нуль не принадлежит этому множеству.
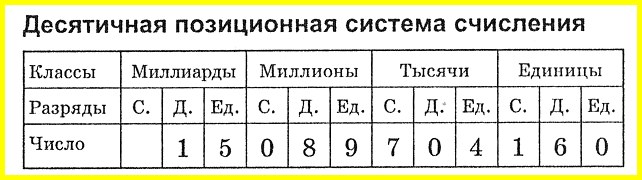
Десятичная система счисления — позиционная система счисления по основанию 10.
Арифметические действия
над натуральными числами
Для натуральных чисел определены следующие действия: сложение, вычитание, умножение, деление, возведение в степень, извлечение корня. Первые четыре действия являются арифметическими.
Пусть a, b и c — натуральные числа, тогда
1. СЛОЖЕНИЕ. Слагаемое + Слагаемое = Сумма
Свойства сложения
1. Переместительное а + b = b + а.
2. Сочетательное а + (b + с) = (а + b) + с.
3. а + 0 = 0 + а = а.
2. ВЫЧИТАНИЕ. Уменьшаемое — Вычитаемое = Разность
Свойства вычитания
1. Вычитание суммы из числа а – (b + с) = а – b – с.
2. Вычитание числа из суммы (а + b) – с = а + (b – с); (а + b) – с = (а – с) + b.
3. а – 0 = а.
4. а – а = 0.
3. УМНОЖЕНИЕ. Множитель * Множитель = Произведение
Свойства умножения
1. Переместительное а • b = b • а.
2. Сочетательное а • (b • с) = (а • b) • с.
3. 1 • а = а • 1 = а.
4. 0 • а = а • 0 = 0.
5. Распределительное (а + b) • с = ас + bс; (а – b) • с = ас – bс.
4. ДЕЛЕНИЕ. Делимое : Делитель = Частное
Свойства деления
1. а : 1 = а.
2. а : а = 1. Делить на ноль нельзя!
3. 0 : а= 0.

Порядок действий
1. Прежде всего действия в скобках.
2. Потом умножение, деление.
3. И только в конце сложение, вычитание.
Делимость натуральных чисел.
Простые и составные числа.
Делителем натурального числа а называется натуральное число, на которое а делится без остатка. Число 1 является делителем любого натурального числа.
Натуральное число называется простым, если оно имеет только два делителя: единицу и само это число. Например, числа 2, 3, 11, 23 — простые числа.
Число, имеющее более двух делителей, называется составным. Например, числа 4, 8, 15, 27 — составные числа.

Признак делимости произведения нескольких чисел: если хотя бы один из множителей делится на некоторое число, то и произведение делится на это число. Произведение 24 • 15 • 77 делится на 12, поскольку множитель этого числа 24 делится на 12.
Признак делимости суммы (разности) чисел: если каждое слагаемое делится на некоторое число, то и вся сумма делится на это число. Если а : b и c : b, то (а + c) : b. А если а : b, а c не делится на b, то a + c не делится на число b.
Если а : c и c : b, то а : b. Исходя из того, что 72 : 24 и 24 : 12, делаем вывод, что 72 : 12.
Представление числа в виде произведения степеней простых чисел называют разложением числа на простые множители.

Основная теорема арифметики: любое натуральное число (кроме 1) либо является простым, либо его можно разложить на простые множители только одним способом.
При разложении числа на простые множители используют признаки делимости и применяют запись «столбиком» В таком случае делитель располагается справа от вертикальной черты, а частное записывают под делимым.
Например, задание: разложить на простые множители число 330. Решение:
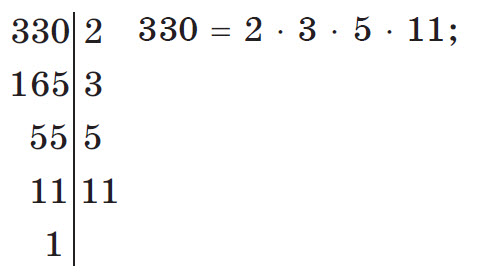
Признаки делимости на 2, 5, 3, 9, 10, 4, 25 и 11.

Признаки делимости на 6, 12, 15, 45
Число делится на 6, если оно одновременно делится на 2 и делится на 3. Например, число 2304. Это число оканчивается на 2, поэтому оно делится на 2. Сумма цифр этого числа равна 2+3+0+4=9, поэтому число делится на 3. Следовательно, число делится на 6.
Число делится на 12, если оно одновременно делится на 3 и делится на 4. Проверяем число 2316. Сумма цифр этого числа равна 2+3+1+6=12, поэтому число делится на 3. Число, составленное из двух последних цифр числа 2316 равно 16, которое делится на 4. Поэтому число 2316 делится на 12.
Число делится на 15, если оно одновременно делится на 3 и делится на 5. Например, число 1470. Сумма цифр равна 1+4+7+0=12, следовательно, число делится на 3. А делимость на 5 обеспечит 0, который стоит на последнем месте. Число 1470 делится на 15.
Число делится на 45, если оно одновременно делится на 5 и на 9, т.е. сумма его цифр кратна 9 и заканчивается оно на 5 или на 0. Проверяем число 180. Сумма цифр этого числа равна 1+8+0=9, поэтому число делится на 9. На конце числа 180 находится 0, следовательно, число делится на 5. Поэтому число 180 делится на 45.
Наибольший общий делитель
Наибольшее натуральное число, на которое делится нацело каждое из двух данных натуральных чисел, называется наибольшим общим делителем этих чисел (НОД). Например, НОД (10; 25) = 5; а НОД (18; 24) = 6; НОД (7; 21) = 7.

Если наибольший общий делитель двух натуральных чисел равен 1, то эти числа называются взаимно простыми.

Алгоритм нахождения наибольшего общего делителя (НОД)

Решение: Нахождение количества учащихся этого класса сводится к нахождению наибольшего общего делителя чисел 155 и 62, поскольку тетради и ручки поделили поровну. 155 = 5 • 31; 62 = 2 • 31. НОД (155; 62) = 31.
Ответ: 31 ученик в классе.
Наименьшее общее кратное
Кратным натурального числа а называется натуральное число, которое делится на а без остатка. Например, число 8 имеет кратные: 8, 16, 24, 32, … Любое натуральное число имеет бесконечно много кратных.
Наименьшее общее кратное (НОК) называется наименьшее натуральное число, которое кратно этим числам.
Алгоритм нахождения наименьшего общего кратного (НОК):

Решение: Количество минут, через которое они снова встретятся на старте, должно делиться на 1 мин,, а также на 45 с. В 1 мин = 60 с. То есть необходимо найти НОК (45; 60).
45 = 32 • 5;
60 = 22 • 3 • 5.
НОК (45; 60) = 22 • 32 • 5 = 4 • 9 • 5 = 180.
В результате получается, что велосипедисты встретятся на старте через 180 с = 3 мин.
Ответ: 3 мин.
Деление с остатком
Если натуральное число а не делится нацело на натуральное число b, то можно выполнить деление с остатком. В таком случае полученное частное называется неполным. Справедливо равенство:
а = b • n + r,
где а — делимое, b — делитель, n — неполное частное, r — остаток. Например, пусть делимое равно 243, делитель — 4, тогда 243 : 4 = 60 (остаток 3). То есть а = 243, b = 4, n = 60, r = 3, тогда 243 = 60 • 4 + 3.
Числа, которые делятся на 2 без остатка, называются четными: а = 2n, n ∈ N.
Остальные числа называются нечетными: b = 2n + 1, n ∈ N.
Это конспект по теме «Натуральные числа. Признаки делимости». Чтобы продолжить, выберите дальнейшие действия:
- Перейти к следующему конспекту: Обыкновенная дробь
- Вернуться к списку конспектов по Математике.
- Проверить знания по Математике.

12 Комментарии
спасибо
Почему в признаке делимости на 11 последний элемент формулы помечен индексом n-1? Я уже плохо помню математику, но мне кажется, индекс должен быть равен просто n. Четные вхождения положительные, нечетные отрицательные. Для n-1 все будет наоборот, и продолжая логическую цепочку будет: +(-1)^(n+1)*An ?
Число делится на 11, если сумма цифр, которые стоят на четных местах равна сумме цифр, стоящих на нечетных местах, либо отличается от неё на 11. Поэтому неважно четные места будут отрицательные или нечетные. Но в одном Вы правы: формула не соответствует примеру. В ближайшее время это исправим.
Почему в первом свойстве вычитания a-(b+c)=a-b-c? Допустим что a- 7, b-6, c-3, тогда получится 7-(6+3)=2 А 7-6-3=-2 разве 2 и -2 равны? Или я что-то путаю?
Сначала выполняется действие в скобках! Поэтому 7-(6+3) = 7-9 = -2. Т.е. в обоих случаях ответ = -2.
В правилах о признака делимости, в строке признак делимости на 25 в примере есть 3 300, т.е. у нас на конце 00, т.е. в этом случае мы берём число состоящее не из 2-х последних цифр, а из 3-х. Наверное стоит дописать и пояснить другие подобные варианты.
Признак делимости исправлен.
Здравствуйте!
Обратите внимание, может, я что-то не так понимаю, уже не так хорошо помню математику.
Тема «Деление с остатком»
Вы пишете, что справедливо равенство а=b*n+r и приводите пример, 243=60*4+3, однако, допустим а=13, b=2, n=0.5, т.е., я имею ввиду, что 13:2=6,5
То равенство а=b*n+r не выходит, мы имеем следующее 13=2*6+0,5, а 2*6+0,5=12,5
Поясните пожалуйста то, что я написал о признаках делимости, прав ли я, и по теме «Деление с остатком», жду ответа, т.к. до конца не понимаю. Спасибо!
Также буду благодарен, если Вы объясните то, что писали о признаках делимости на 6, 15, 45 и т. д., то есть на числа, произведение которых можно разложить на множители 2, 3, 5, 9 и 10. Буквально один пример, как рассуждать, до конца не понял.
Статья дополнена разделом «Признаки делимости на 6, 12, 15, 45»
0,5 и 6,5 — не являются натуральными числами. Указанное равенство только для натуральных чисел!
В признаках деления на 15 написано «Число делится на 15, если оно одновременно делится на 3 и делится на 5. Например, число 1470. Сумма цифр равна 1+4+7+0=12, следовательно, число делится на 3. А делимость на 5 обеспечит 0, который стоит на последнем месте. Число 1470 делится на 12.» В конце не 15 а 12