Итоговая контрольная работа по геометрии в 7 классе с ответами УМК Атанасян Просвещение (средний уровень). Урок 68 поурочного планирования по геометрии. Геометрия 7 Атанасян К-6 Уровень 2 (варианты 3, 4). Цитаты использованы в учебных целях.
Смотреть Список всех контрольных по геометрии в 7 классе по УМК Атанасян.
Другие варианты итоговой контрольной работы в 7 классе:
Итоговая контрольная работа по геометрии
Уровень 2 (средний). Геометрия 7 класс
Вариант 3
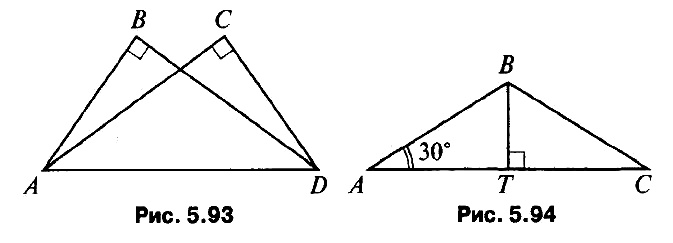
- Дано: ∠B = ∠C = 90°, ∠ADC = 50°, ∠ADB = 40° (рис. 5.93). Доказать: ΔABD = ΔDCA.
- В равнобедренном треугольнике угол между боковыми сторонами в три раза больше угла при основании. Найдите углы треугольника.
- Параллельные прямые а и b пересечены двумя параллельными секущими АВ и CD, причем точки А и С лежат на прямой а, а точки В и D — на прямой b. Доказать: АС = BD.
- * Дано: АВ = ВС, ВТ = 4 см (рис. 5.94).
а) Между какими целыми числами заключена длина отрезка АС?
б) Найдите сумму длин отрезков, соединяющих точку Т с серединами сторон АВ и ВС.
Вариант 4
- Дано: ∠B = ∠C = 90°, ∠ADB = 40°, ∠BDC = 10° (рис. 5.95). Доказать: ΔABD = ΔDCA.
- В равнобедренном треугольнике угол при основании в четыре раза больше угла между боковыми сторонами. Найдите углы треугольника.
- Параллельные прямые а и b пересечены двумя параллельными секущими АВ и CD, причем точки А и С принадлежат прямой а, а точки В и D — прямой b. Доказать: АВ = CD.
- * Дано: АВ = ВС, АС = 10 см (рис. 5.96).
а) Между какими целыми числами заключена длина высоты AВС?
б) Найдите сумму длин отрезков, соединяющих точку Т с серединами сторон АВ и ВС.
Решения и ответы на контрольную работу:
ОТВЕТЫ на Вариант 3
№ 1. Сумма острых углов прямоугольного треугольника равна 90°.
ΔADC: ∠ACD = 90°, ∠ADC = 50°, ⇒ ∠ ACD = 90° — 50° = 40°
В прямоугольных треугольниках ABD и DCA общая гипотенуза AD и одинаковые острые углы (∠ACD = ∠ADB = 40°), ⇒ ΔABD = ΔDCA по гипотенузе и острому углу.
№ 2. В равнобедренном треугольнике углы при основании равны. А сумма углов треугольника равна 180°. Будем решать алгебраическим способом. Для удобства, назовем треугольник ABC, а бОльшим будем угол A.
Пусть угол В = х. Тогда угол С= х, а угол А равен 3х (в три раза больше). Их сумма равна х+х+3х. А по теореме суммы углов треугольника 180°. Составим уравнение: х + х + 3х = 180. Решив уравнение получим: х = 36.
Значит, угол В (при основании) равен 36°, угол С (тоже при основании) равен 36°, а угол А = 36 • 3 = 108°
Ответ: углы треугольника равны 36°, 36° и 108°.
№ 3. По условию параллельные прямые а и b пересекаются двумя параллельными секущими АВ и СD, в результате этого получается четырехугольник АВСD, в котором пары противолежащих сторон АВ и СD, АС и ВD (принадлежащие прямым а и b) параллельны, значит полученный четырехугольник АВСD является параллелограммом. Противолежащие стороны параллелограмма равны, значит АС = BD, что и требовалось доказать.
№ 4. а) между числами 13 и 14.
ОТВЕТЫ на Вариант 4
№ 1. а) ∠ADC = ∠ADB + ∠BDC = 40° + 10 °= 50°. б) ∠BAD = 180 — ∠ABD — ∠ADB = 180° — 90° — 40° = 50°. в) ∠BAD = ∠ADC = 50°; ∠ABD = ∠ACD = 90°; гипотенуза AD общая. Отсюда следует, что треугольники равны (если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого, то такие треугольники равны).
№ 2. Пусть ∠A и ∠С – углы при основании, а ∠В – угол между боковыми сторонами. Так как треугольник равнобедренный, то ∠A = ∠C. Угол В обозначим х, тогда ∠A = ∠C = 4х. Составим уравнение: x + 4x + 4x = 180°. Отсюда следует, что x = 20° = ∠B. Тогда ∠A = 4 • 20 = 80° = ∠C. Ответ: углы треугольника равны 80°, 80° и 20°.
№ 3. Проведем диагональ AD и докажем, что △ABD = △ACD. Так как a параллельно b, значит накрест лежащие углы равны: ∠BAD = ∠ADC и ∠BDA = ∠CAD. AD — общая, значит △ABD = △ACD по стороне и прилежащим углам. Следовательно, AB = CD
№ 4. a) Между числами 8 и 9.
Информация для учителя:
По прохождении каждой темы предусмотрена контрольная работа, состоящая из заданий трех уровней сложности, которые определяются или учителем, или самим учащимся (при этом число экземпляров вариантов должно быть достаточным). Разумеется, учащиеся должны знать о различной сложности вариантов и критериях оценки контрольной работы.
Контрольная работа составлена в 6 вариантах различной сложности (варианты 1, 2 самые простые, варианты 3, 4 сложнее и варианты 5, 6 самые сложные). При этом сложность вариантов нарастает не очень резко. Каждый вариант содержит 6 задач примерно одинаковой сложности (может быть, несколько сложнее две последние задачи).
Другие варианты итоговой контрольной работы в 7 классе:
Вы смотрели: Итоговая контрольная работа по геометрии в 7 классе с ответами УМК Атанасян Просвещение (средний уровень). Урок 68 поурочного планирования по геометрии. Геометрия 7 Атанасян К-6 Уровень 2 (варианты 3, 4).
Смотреть Список всех контрольных по геометрии в 7 классе по УМК Атанасян.
В учебных целях использованы цитаты из учебного пособия «Поурочные разработки по геометрии. 7 класс / Гаврилова Н.Ф. — М.: ВАКО», которое используется в комплекте с учебником «Атанасян Л.С., Бутузов В.Ф. и др. Геометрия. 7—9 классы. Учебник для общеобразовательных организаций. М.: Просвещение».


3 Комментарии
Вариант 3.
Дано: ∠B = ∠C = 90°, ∠ADC = 50°, ∠ADB = 40° (рис. 5.93). Доказать: ΔABD = ΔDCA.
В равнобедренном треугольнике угол между боковыми сторонами в три раза больше угла при основании. Найдите углы треугольника.
Параллельные прямые а и b пересечены двумя параллельными секущими АВ и CD, причем точки А и С лежат на прямой а, а точки В и D — на прямой b. Доказать: АС = BD.
* Дано: АВ = ВС, ВТ = 4 см (рис. 5.94).
а) Между какими целыми числами заключена длина отрезка АС?
б) Найдите сумму длин отрезков, соединяющих точку Т с серединами сторон АВ и ВС.
Палеограмм в 7 класс нет!
тогда получается что задача номер 3 из 3 вариант нерешаемая . Исправьте ошибку
можно решить не используя параллелограмм, провести диагональ и решить используя признаки равенства треугольников