«Равнобедренный треугольник
+ ЗАДАЧИ по теме»

Равнобедренный треугольник — треугольнику которого две стороны равны.
Равные стороны называют боковыми сторонами, а третью сторону — основанием.

Свойства равнобедренного треугольника были известны с давних времен. Еще древние вавилоняне (II в. до н.э.) знали, что углы у основания равнобедренного треугольника равны. Любой треугольник можно разрезать на равнобедренные треугольники.

Свойства и признаки равнобедренного треугольника

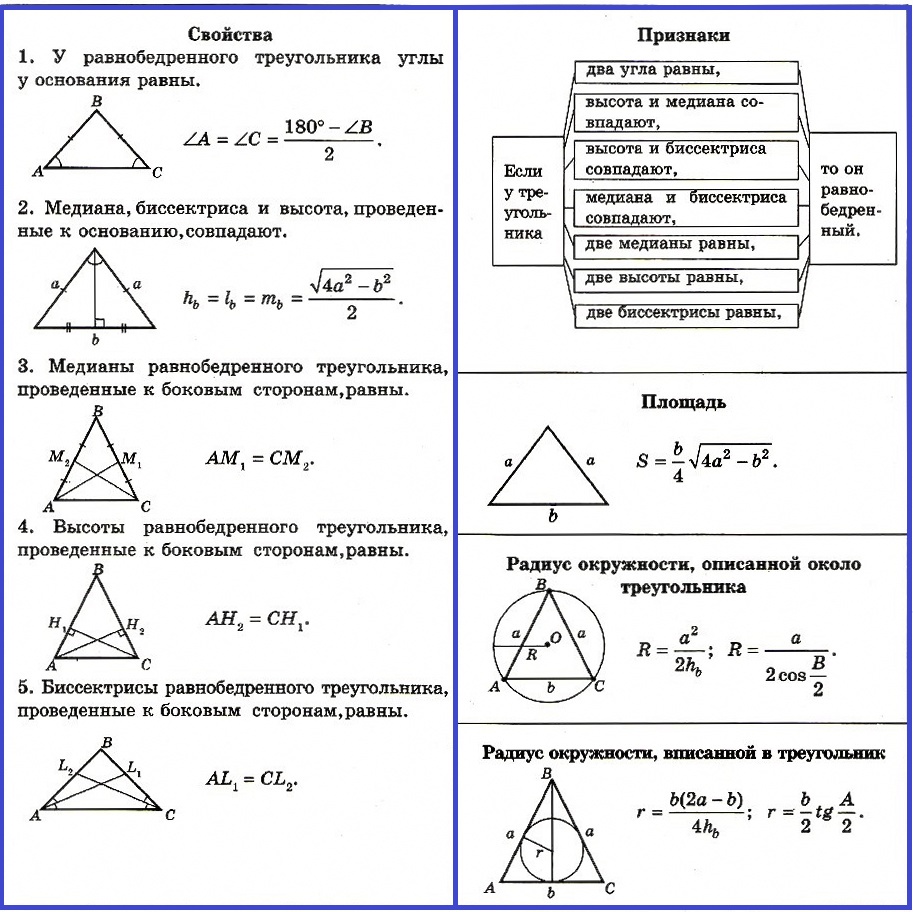
Свойства равнобедренного треугольника:
1. У равнобедренного треугольника углы у основания равны (теорема).
2. Медиана, биссектриса и высота, проведенные к основанию, совпадают (теорема).
3. Медианы равнобедренного треугольника, проведенные к боковым сторонам, равны.
4. Высоты равнобедренного треугольника, проведенные к боковым сторонам, равны.
5. Биссектрисы равнобедренного треугольника, проведенные к боковым сторонам, равны.

Признаки равнобедренного треугольника: 
Если у треугольника есть один из нижеуказанных признаков, то он равнобедренный:
— два угла равны,
— высота и медиана совпадают,
— высота и биссектриса совпадают,
— медиана и биссектриса совпадают,
— две медианы равны,
— две высоты равны,
— две биссектрисы равны.

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ:

Уважаемые учителя!

Ранее размещенные здесь материалы удалены по требованию Издательства «Аверсэв» от 20 октября 2022 года. Кроме того, указанные материалы содержали ошибки, опечатки и не соответствовали ФГОС. В связи с этим не рекомендуем пользоваться учебными пособиями Издательства «Аверсэв» (Беларусь). Мы поддерживаем позицию этого издательства, что бесплатно рекламировать их учебные пособия нельзя, пусть рекламируют свои книги только за большие деньги, только через рекламу, только по предоплате!

Задача № 1. Периметр равнобедренного треугольника равен 65 см, а основание относится к боковой стороне как 3:5. Найдите стороны этого треугольника.

Решение. А, В, С — вершины треугольника. По условию задачи АС : АВ = 3 : 5. Следовательно, АС = 3АВ/5.
Дальнейшие вычисления производим, воспользовавшись формулой расчёта периметра треугольника:
АС + АВ + ВС = 65 сантиметров.
ВС = АВ, так как данный треугольник равнобедренный.
Подставляем в исходную формулу АВ вместо ВС и 3АВ/5 вместо АС:
3АВ/5 + 2АВ = 65.
13АВ/5 = 65.
13АВ = 5 • 65.
АВ = 25 сантиметров.
АС = 25 х 3 : 5 = 15 сантиметров.
Ответ: АС = 15 сантиметров, АВ = ВС =25 сантиметров.

Задача № 2. В треугольнике АВС проведена биссектриса ВМ, ∠ВАК = 70°, ∠АКС = 110°. Докажите, что ВМ ⊥ АК.

Задача № 3. Дано: ΔKLM – равносторонний, ΔKNM – равнобедренный (KN = MN), KM – общая сторона, P_KNM > P_KLM в 1,5 раза, LM = 8 см. Найти: MN.

Решение.
1) Так как △KLM — равносторонний, значит, KL = LM = KM = 8 см, следовательно, Р_KLM = 3 * LM = 3 * 8 = 24 (см);
2) так как P_KNM > Р_KLM в 1,5 раза, следовательно, P_KNM = 1,5 • Р_KLM = 1,5 • 24 = 36 (см).
Так как △KNM — равнобедренный, следовательно, Р_KNM = KM + 2MN,
KM = 8 см  => P_KNM = 36 см.
Составим уравнение: 36 = 8 + 2 • MN  => 2 • MN = 28  => MN = 14 (см).
Ответ: MN = 14 см.

Задача № 4. Постройте равнобедренный треугольник, если даны прямая, на которой лежит медиана, проведенная из вершины, две точки на боковых сторонах и точка на основании.

Теоретический тест
с последующей самопроверкой

1. Медиана в равнобедренном треугольнике является его биссектрисой и высотой. Это утверждение:
   а) всегда верно;
   б) может быть верно;
   в) всегда неверно.
2. Если треугольник равносторонний, то:
   а) он равнобедренный;
   б) все его углы равны;
   в) любая его высота является биссектрисой и медианой.
3. В каком треугольнике только одна его высота делит треугольник на два равных треугольника?
   а) в любом;
   б) в равнобедренном;
   в) в равностороннем.
4. Биссектриса в равностороннем треугольнике является медианой и высотой. Это утверждение:
   а) всегда верно;
   б) может быть верно;
   в) всегда неверно.
5. Если треугольник равнобедренный, то:
   а) он равносторонний;
   б) любая его медиана является биссектрисой и высотой;
   в) два его угла равны.
6. В каком треугольнике любая его высота делит треугольник на два равных треугольника?
   а) в любом;
   б) в равнобедренном;
   в) в равностороннем.
7. Если в треугольнике два угла равны, то этот треугольник является:
   а) равносторонним;
   б) равнобедренным;
   в) прямоугольным.
8. Если в треугольнике две стороны равны, то:
   а) у него равны два угла;
   б) у него все углы равны;
   в) этот треугольник равносторонний.

Вы смотрели конспект по теме «Равнобедренный треугольник + ЗАДАЧИ по теме». Выберите дальнейшие действия:

• Смотреть самостоятельную работу с ответами на тему «Равнобедренный треугольник»
• Перейти к следующему конспекту: Свойства сторон и углов треугольника + ЗАДАЧИ по теме
• Вернуться к Списку конспектов по геометрии