Треугольник. Равенство треугольников

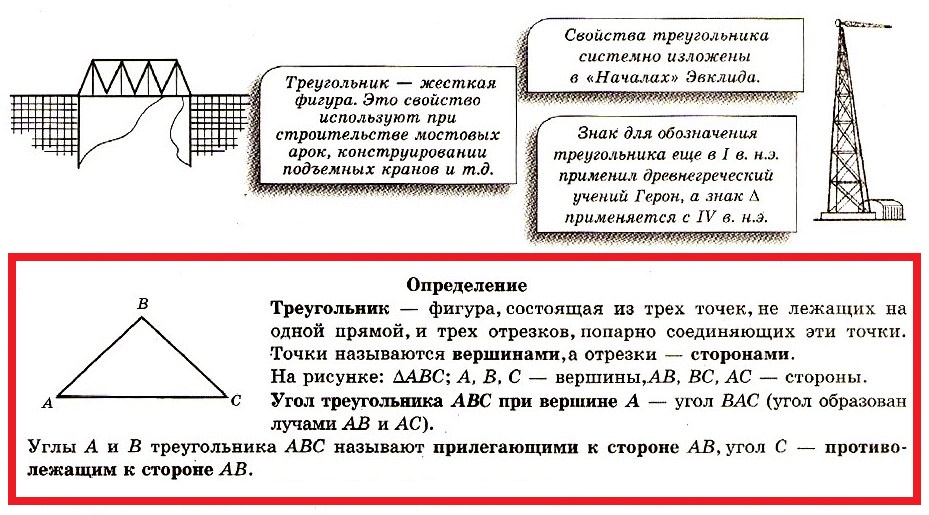
Треугольник — фигура, состоящая из трех точек, не лежащих на одной прямой, и трех отрезков, попарно соединяющих эти точки. Точки называются вершинами, а отрезки — сторонами.

Треугoльник — жесткая фигура. Это свойство используют при строительстве мостовых арок, конструировании подъемных кранов и т.д. Свойства треугольника системно изложены в «Началах» Эвклида. Знак для обозначения треугольника еще в I в. н.э. применил древнегреческий учений Герон, а знак Δ применяется с IV в. н.э.

Медиана, биссектриса и высота треугольника

Медианой треугольника называется отрезок, соединяющий вершину треугольника с серединой противоположной стороны.
Медиана делит стороны пополам. Три медианы треугольника пересекаются в одной точке и в этой точке делятся в отношении 2:1, считая от вершины.

Биссектриса треугольника делит угол пополам. Биссектриса угла треугольника делит противоположную сторону в отношении длин прилежащих сторон. Три биссектрисы пересекаются в одной точке, которая является центром окружности, вписанной в треугольник.

Высотой треугольника называется отрезок, опущенный из вершины треугольника на противоположную сторону. В тупоугольном треугольнике высота опускается на продолжение стороны. Три высоты треугольника всегда пересекаются в одной точке. В случае тупого угла в одной точке пересекаются продолжения высот.

Равные треугольники

Два треугольника называются равными, если их можно совместить наложением.

Аксиома существования треугольника, равного данному.
Каким бы ни был треугольник, существует треугольник, равный ему в заданном расположении относительно данной полупрямой.

Свойства равных треугольников
1. В равных треугольниках соответствующие стороны равны.
2. В равных треугольниках соответствующие углы равны.
3. Периметры равных треугольников равны.
4. Площади равных треугольников равны.
5. Против равных сторон лежат равные углы.
6. Против равных углов лежат равные стороны.

Признаки равенства треугольников

Признаки равенства треугольников — одна из основных теорем геометрии. Треугольник на евклидовой плоскости однозначно можно определить по следующим тройкам основных элементов:

• Первый признак — по двум сторонам и углу между ними.
• Второй признак – по двум углам и прилежащей стороне.
• Третий признак – по трём сторонам.

Дополнительные признаки равенства
• Если две стороны и медиана, проведенная к третьей стороне треугольника, соответственно равны двум сторонам и медиане, проведенной к третьей стороне другого треугольника, такие треугольники равны.
• Если два угла и высота,проведенная к стороне, к которой прилегают эти углы, одного треугольника, соответственно равны двум углам и высоте, проведенной к стороне, к которой прилегают эти углы, другого треугольника, то такие треугольники равны.
• Если сторона, высота и медиана, проведенные к стороне одного треугольника, соответственно равны стороне, высоте и медиане, проведенным к этой стороне другого треугольника, то эти треугольники равны.
• Если медиана и углы, на которые она делит угол, одного треугольника, соответственно равны медиане и углам,на которые она делит угол, другого треугольника, эти треугольники равны.

Это конспект по геометрии на тему «Треугoльник. Равенство треугольников». Выберите дальнейшие действия:

• Перейти к следующему конспекту: ЗАДАЧИ на Признаки равенства треугольников
• Вернуться к Списку конспектов по геометрии