Контрольная работа № 6 «Дробные рациональные уравнения» с ответами и решениями. УМК Макарычев. Алгебра 8 класс (Просвещение). Поурочное планирование по алгебре для 8 класса. ГЛАВА III. КВАДРАТНЫЕ УРАВНЕНИЯ. § 9. Дробные рациональные уравнения (11 ч). Урок 63. Контрольная работа № 6 по теме «Квадратные уравнения. Дробные рациональные уравнения» + ОТВЕТЫ и РЕШЕНИЯ. Информация для учителей и родителей.

Смотреть Список всех контрольных по алгебре в 8 классе по УМК Макарычев

Контрольная работа № 6
«Дробные рациональные уравнения»

Цель: проверить знания, умения и навыки учащихся по теме.
Тип урока: урок контроля, оценки и коррекции знаний.

ХОД УРОКА

I. Сообщение темы и цели урока

II. Общая характеристика контрольной работы

Контрольная работа составлена в 6 вариантах различной сложности (варианты 1, 2 самые простые, варианты 3, 4 сложнее и варианты 5, 6 самые сложные). При этом сложность вариантов нарастает не очень резко. Каждый вариант содержит 6 задач примерно одинаковой сложности (может быть, несколько сложнее две последние задачи).

При проверке вариантов 1, 2 оценка «5» ставится за правильное решение пяти задач, оценка «4» — четырех задач и оценка «3» — трех задач. Одна задача является резервной (или запасной) и дает некоторую свободу выбора учащимся. При таких же критериях оценки за решение задач вариантов 3, 4 дается дополнительно 0,5 балла, вариантов 5, 6 — 1 балл (т. е. оценку «5» можно получить за правильное решение четырех задач).

III. Контрольная работа в 6 вариантах

IV. Подведение итогов контрольной работы

1. Распределение работ по вариантам и результаты решения. Данные о результатах работы удобно заносить в таблицу (для каждой пары вариантов).

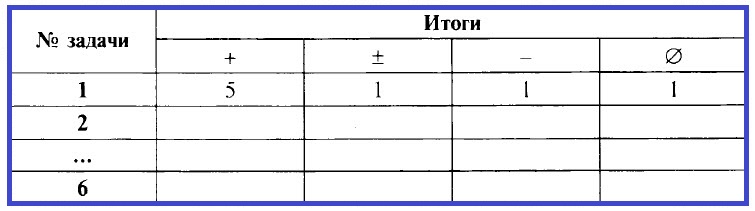
Обозначения:
+ (число решивших задачу правильно или почти правильно);
± (число решивших задачу со значительными погрешностями);
– (число не решивших задачу);
∅ (число не решавших задачу).

2. Типичные ошибки, возникшие при решении задач.
3. Наиболее трудные задачи и их разбор (учителем или школьниками, решившими их).
4. Разбор всей контрольной работы (вывесить на стенде ответы к заданиям и разобрать наиболее трудные варианты).

V. Разбор задач (ответы и решения)

VI. Подведение итогов урока

Вы смотрели: Поурочное планирование по алгебре для 8 класса. УМК Макарычев (Просвещение). ГЛАВА III. КВАДРАТНЫЕ УРАВНЕНИЯ. § 9. Дробные рациональные уравнения (11 ч). Урок 63. Контрольная работа № 6 «Дробные рациональные уравнения» + ОТВЕТЫ и РЕШЕНИЯ.

Смотреть Список всех контрольных по алгебре в 8 классе по УМК Макарычев

Вернуться к Списку уроков Тематического планирования в 8 классе.