
Задачи на простые механизмы с решениями
Формулы, используемые на уроках «Задачи на простые механизмы,
условия равновесия рычага, блоки, золотое правило механики».
Название величины |
Обозначение |
Единица измерения |
Формула |
Сила |
F |
Н |
F1l1 = F2l2 |
Плечо силы |
l |
м |
|
Момент силы |
M |
Нм |
M = Fl |
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача № 1. С помощью рычага рабочий поднимает плиту массой 120 кг. Какую силу он прикладывает к большему плечу рычага, равному 2,4 м, если меньшее плечо 0,8 м?

Задача № 2. На концах рычага действуют силы 20 Н и 120 Н. Расстояние от точки опоры до большей силы равно 2 см. Определите длину рычага, если рычаг находится в равновесии.

Задача № 3. На рисунке изображен рычаг, имеющий ось вращения в точке О. Груз какой массы надо подвесить в точке В для того, чтобы рычаг был в равновесии?

Задача № 4. На меньшее плечо рычага действует сила 300 Н, на большее — 20 Н. Длина меньшего плеча 5 см. Определите длину большего плеча.

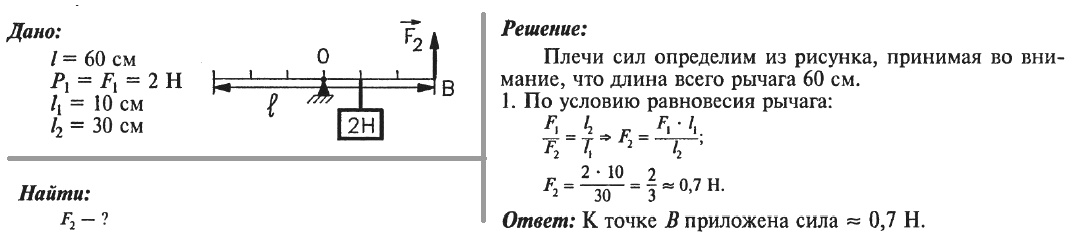
Задача № 5. Рычаг длиной 60 см находится в равновесии. Какая сила приложена в точке В?
Задача № 6. Момент силы действующей на рычаг, равен 20 Н*м. Найти плечо силы 5 Н, если рычаг находится в равновесии.

Задача № 7. Какое усилие необходимо приложить, чтобы поднять груз 1000 Н с помощью подвижного блока? Какая совершится работа при подъеме груза на 1 м? (Вес блока и трение не учитывать).

Задача № 8. Система блоков находится в равновесии. Определите вес правого груза. (Вес блоков и силу трения не учитывать).

Задача № 9. При помощи подвижного блока поднимают груз, прилагая силу 105 Н. Определите силу трения, если вес блока равен 20 Н, а вес груза 180 Н.

Задача № 10. ОГЭ Стержень цилиндрической формы длиной l = 40 см состоит на половину своей длины из свинца и наполовину — из железа. Найти расстояние от центра тяжести до центра симметрии стержня. Плотность свинца p1 = 11,4 г/см3, плотность железа p2 = 7,8 г/см3.
Решение. Центр тяжести тела (центр масс) — точка приложения силы притяжения его к земле — веса тела P. У тел, имеющих какую-либо симметрию, он совпадает с центром симметрии. Например, у однородного цилиндра центр тяжести расположен на его оси в центре цилиндра. Тело, закреплённое на оси, проходящей через его центр тяжести, находится в состоянии безразличного равновесия. Мысленно закрепим стержень AB на оси, перпендикулярной стержню и проходящей через его центр тяжести C, отстоящий от его геометрического центра O на расстояние x в сторону более тяжёлой половины стержня. Центры инерций половинок размещены на расстояниях l/4 от середины стержня.
х = (11,4–7,8)/(11,4+7,8) • 0,4/4 = 0,01875 ≈ 0,019 (м)
Ответ: 1,9 см.
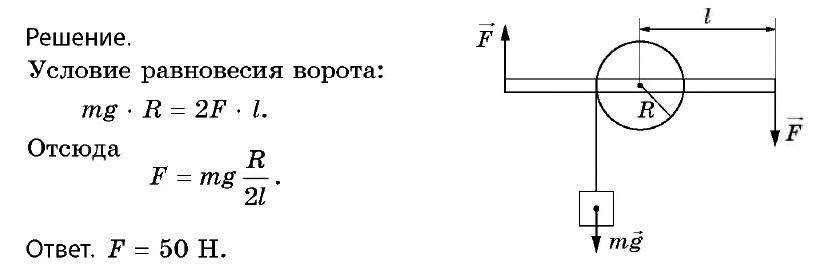
Задача № 11. ЕГЭ Масса якоря корабля m = 50 кг. Радиус барабана, на который наматывают якорную цепь, R = 0,2 м, длина каждой из двух ручек ворота l = 1 м. Какую силу нужно приложить к каждой из них, чтобы поднять якорь?
Краткая теория для решения задачи на простые механизмы.

Конспект урока «Задачи на простые механизмы с решениями».
Следующая тема: «Задачи на КПД простых механизмов».

20 Комментарии
опечатка, в 10м номере L/2, а не L/4 т.к половина
Опечатки нет. Центры инерций половинок размещены на расстояниях l/4 от середины стержня.
Хорошие задачи!!!!
Задание №2. Решить задачи: (за каждое решение дается 2 балла)
1) На рычаг действует сила 100 Н. Чему равен момент этой силы, если плечо силы 5 м?
2) С помощью рычага рабочий поднимает груз весом P=F1= 2000 Н. Какую силу F2 он прикладывает к большему плечу рычага длиной d2= 4 м, если меньшее плечо равно d1= 1 м?
Помогите
1)Дано: Решение:
F1=100H. по формуле M=Fd
d1=5м. M=100H*5м=500Нм
M=? Ответ:500Нм
2)P=F1=2000H по формуле F1/F2=d2/d1
d1=1м. F2=F1*d1/d2=2000Н*1м/4м=500Н
d2=4м
F2=? Ответ:500Н
1)20
2)500Н
жду балы
спасибо, мне теперь это всё переписать нужно за 1 день
На рычаг с неподвижной осью О действуют силы F1 = 4Н и F2. Определить модуль силы F2, необходимой для того, чтобы удержать рычаг в равновесии, если углы α = 45°,
β = 120°, длины АО = 0,5 м, ВО = 0,6 м. (Ответ 2,72)
В 11 задаче я использовал формулу l/r и выйгрыш в силе был равен 5 потомнашел силу тяжести груза и разделил на 5 но ответ не верный, почему эта формула не подходит?
Потому что на рычаг действуют две силы с двух сторон
Почему в первой задаче ускорение свободного падения 10 а не 9,8?
так удобнее считать
g=9,8 м/с²
Но, в большинство задачах что-бы упростить решение, «g» берут как g≈10 м/с² и это считается правильно. Так как это дано в задаче.
Полностью с Вами согласен. Способ округления в физике часто применяется в подобных задачах. Даже если взять самую простую:
Камень падал вниз примерно 5 — 6 секунд ( как в жизни). Решение:
g=10 м/с2
6(5)с * 10 м/с = примерно от 50 до 60 ( м ) — глубина. Если бы g = 9,8 м/с2, примерный ответ был бы одинаковый, но добавилось бы лишнее округление.
В 11 задании применяется условие равновесия ворота, так вот, его можно как-то самому выразить, или это очень сложно и лучше тупо запомнить?
Там цепь по касательной к «вертелю» направлена. Т.е угол 90⁰, поэтому, собственно, радиус и есть плечо. А про ручки от «вертеля», думаю, понятно. Ручки две. Сила к каждой одинакова, а значит сила для поднятия якоря/2
извините, не могли бы вы объяснить поподробнее 1 и 2 предложение? я не совсем понял, что вы имеете ввиду.
в 11 задании, в решении, где
mg * r = 2F * l
почему l не умножается на 2? плеч, как и ручек 2.
У нас именно 2 МОМЕНТА СИЛ, а не 2 силы и 2 плеча, в уравнении мы рассматриваем так
спасибо