«Мерзляк Геометрия 8 Глава 1»
Мерзляк Геометрия 8 Глава 1 — это краткий конспект учебника по геометрии за 8 класс (А.Г.Мерзляк и др.) в 4-х частях. Цитаты из учебника помогут учащимся, которые сдали учебник в библиотеку при переходе в старший класс, быстро освежить знания, полученные в 8 классе. Часть 1-я «Четырехугольники».
Глава 1. Четырехугольники
§ 1. Четырёхугольник и его элементы




§ 2. Параллелограмм. Свойства параллелограмма


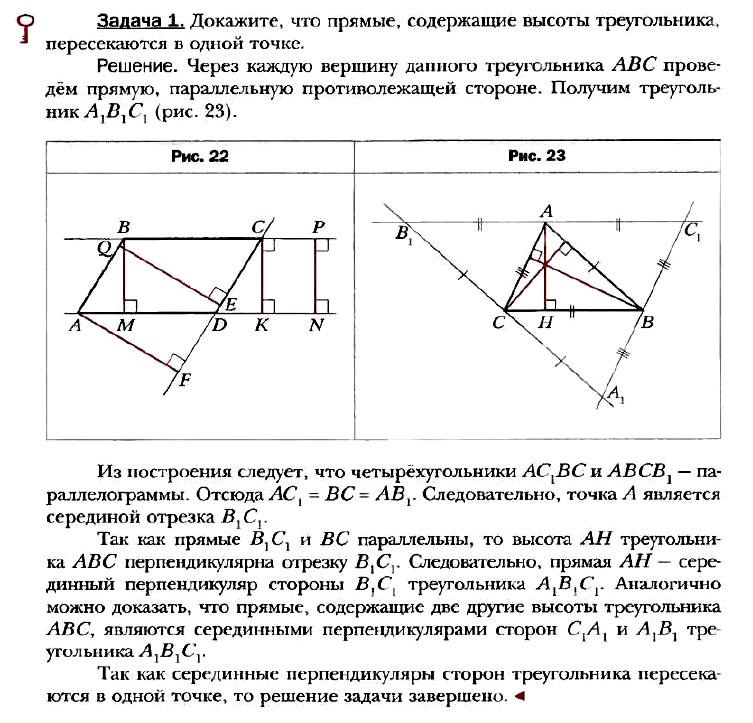
§ 3. Признаки параллелограмма


§ 4. Прямоугольник


§ 5. Ромб


§ 6. Квадрат

§ 7. Средняя линия треугольника


§ 8. Трапеция




§ 9. Центральные и вписанные углы




§ 10. Описанная и вписанная окружности четырехугольника




ИТОГИ ГЛАВЫ 1
«Мерзляк Геометрия 8 Глава 1» СОДЕРЖАНИЕ: § 1. Четырёхугольник и его элементы. § 2. Параллелограмм. Свойства параллелограмма. § 3. Признаки параллелограмма. § 4. Прямоугольник. § 5. Ромб. § 6. Квадрат. § 7. Средняя линия треугольника. § 8. Трапеция. § 9. Центральные и вписанные углы. § 10. Описанная и вписанная окружности четырехугольника.
Сумма углов четырёхугольника
Сумма углов четырёхугольника равна 360°.
Параллелограмм
Параллелограммом называют четырёхугольник, у которого каждые две противолежащие стороны параллельны.
Свойства параллелограмма
• Противолежащие стороны параллелограмма равны.
• Противолежащие углы параллелограмма равны.
• Диагонали параллелограмма точкой пересечения делятся пополам.
Высота параллелограмма
Высотой параллелограмма называют перпендикуляр, опущенный из любой точки прямой, содержащей сторону параллелограмма, на прямую, содержащую противолежащую сторону.
Признаки параллелограмма
• Если в четырёхугольнике каждые две противолежащие стороны равны, то этот четырёхугольник — параллелограмм.
• Если в четырёхугольнике две противолежащие стороны равны и параллельны, то этот четырёхугольник — параллелограмм.
• Если в четырёхугольнике диагонали точкой пересечения делятся пополам, то этот четырёхугольник — параллелограмм.
Прямоугольник
Прямоугольником называют параллелограмм, у которого все углы прямые.
Особое свойство прямоугольника
Диагонали прямоугольника равны.
Признаки прямоугольника
• Если один из углов параллелограмма прямой, то этот параллелограмм — прямоугольник.
• Если диагонали параллелограмма равны, то этот параллелограмм — прямоугольник.
Ромб
Ромбом называют параллелограмм, у которого все стороны равны.
Особое свойство ромба
Диагонали ромба перпендикулярны и являются биссектрисами его углов.
Признаки ромба
• Если диагонали параллелограмма перпендикулярны, то этот параллелограмм — ромб.
• Если диагональ параллелограмма является биссектрисой его угла, то этот параллелограмм — ромб.
Квадрат
Квадратом называют прямоугольник, у которого все стороны равны.
Средняя линия треугольника
Средней линией треугольника называют отрезок, соединяющий середины двух его сторон.
Свойство средней линии треугольника
Средняя линия треугольника, соединяющая середины двух его сторон, параллельна третьей стороне и равна её половине.
Трапеция
Трапецией называют четырёхугольник, у которого две стороны параллельны, а две другие не параллельны.
Высота трапеции
Высотой трапеции называют перпендикуляр, опущенный из любой точки прямой, содержащей одно из оснований на прямую, содержащую другое основание.
Средняя линия трапеции
Средней линией трапеции называют отрезок, соединяющий середины боковых сторон трапеции.
Свойство средней линии трапеции
Средняя линия трапеции параллельна основаниям и равна их полусумме.
Центральный угол окружности
Центральным углом окружности называют угол с вершиной в центре окружности.
Вписанный угол окружности
Вписанным углом окружности называют угол, вершина которого лежит на окружности, а стороны пересекают окружность.
Градусная мера вписанного угла окружности
Градусная мера вписанного угла равна половине градусной меры дуги, на которую он опирается.
Свойства вписанных углов
• Вписанные углы, опирающиеся на одну и ту же дугу, равны.
• Вписанный угол, опирающийся на диаметр (полуокружность), — прямой.
Окружность, описанная около четырёхугольника
Окружность называют описанной около четырёхугольника, если она проходит через все его вершины.
Свойство вписанного в окружность четырёхугольника
Если четырёхугольник является вписанным в окружность, то сумма его противолежащих углов равна 180°.
Признак четырёхугольника, около которого можно описать окружность
Если в четырёхугольнике сумма противолежащих углов равна 180°, то около него можно описать окружность.
Окружность, вписанная в четырёхугольник.
Окружность называют вписанной в четырёхугольник, если она касается всех его сторон.
Свойство описанного около окружности четырёхугольника.
Если четырёхугольник является описанным около окружности, то суммы его противолежащих сторон равны.
Признак четырёхугольника, в который можно вписать окружность.
Если в выпуклом четырёхугольнике суммы противолежащих сторон равны, то в него можно вписать окружность.
Смотреть другие главы учебника:
Это конспект по теме «Мерзляк Геометрия 8 Глава 1». Вернуться к Списку конспектов по геометрии.

1 Комментарий
Большое и искреннее спасибо! Это действительно — очень ценная книга, в которой очень удобно выделена в отдельную часть теория из учебника, в котором теория и задачи размещены вперемежку…Здоровья вам!